⚛️ When Physics Becomes the Algorithm
What Quantum AI Means for the Rest of Us
Entangled whispers—
minds linked beyond space, beyond words.
Physics learns to trust.
With every article and podcast episode, we provide comprehensive study materials: References, Executive Summary, Briefing Document, Quiz, Essay Questions, Glossary, Timeline, Cast, FAQ, Table of Contents, Index, Polls, 3k Image, Fact Check, Comic and
Street Art at the very bottom of the page.
Soundbite
Essay
We live in a world where technology promises to solve everything, yet somehow makes everything more complicated. Every few years, we’re told about the next revolutionary breakthrough—blockchain, the metaverse, whatever buzzword venture capitalists are currently salivating over. Most of these revolutions turn out to be expensive ways to do things we were already doing, just with more energy consumption and investor presentations.
But occasionally, something genuinely different emerges. Something that doesn’t just optimize existing systems but fundamentally reimagines how systems could work. The convergence of quantum computing and artificial intelligence might actually be one of those rare moments. And unlike most technological revolutions that promise to “disrupt” our lives (usually code for “make things worse while extracting more value”), this one hints at solving problems we’ve created with our previous solutions.
Here’s the uncomfortable truth about modern AI: it’s built on a foundation of centralization and surveillance. When we talk about machine learning systems getting smarter, we’re really talking about massive corporations hoovering up unimaginable amounts of data, funneling it into centralized servers, and processing it in ways that make our privacy concerns look quaint. The computational power is impressive. The ethical framework is horrifying.
The researchers whose work forms the basis of this deep dive—Ratun Rahman, Dinsin Grian, Christo Karisimutal Thomas, Alexander Daru, and Waleed Saad—weren’t trying to build a better surveillance machine. They were trying to solve a genuinely thorny problem: how do you create AI systems that are both powerful and respectful of privacy? How do you enable collaboration without coercion? How do you build intelligence that doesn’t require everyone to surrender their data to a central authority?
Their answer involves something called Quantum Federated Learning, and it’s worth understanding because it represents a different philosophy of how technology could work.
The Privacy Problem We’ve Normalized
We’ve become so accustomed to the surveillance economy that we barely notice it anymore. Every app, every device, every “smart” system operates on the assumption that your data belongs to whoever can collect it. Want better recommendations? Hand over your browsing history. Want personalized healthcare? Upload your medical records. Want your city to run more efficiently? Let us track your every movement.
The classical approach to machine learning requires this centralization. You need massive datasets in one place to train effective models. But this creates what security experts call a “single point of failure”—a honeypot of valuable information just waiting to be breached, hacked, or subpoenaed.
Federated Learning was the first attempt to solve this. Instead of sending your data to a central server, the server sends a model to your device. Your device trains the model on your local data, then sends back only the updated model parameters—not the raw data itself. It’s a clever workaround, and it’s already being used by companies like Google for features like predictive text on your phone.
But there’s a problem. Classical Federated Learning still has limitations. The models can be reverse-engineered to expose private information. The communication overhead is massive. And perhaps most importantly, it doesn’t scale well to the truly complex problems we need AI to solve—problems in medicine, climate modeling, materials science, and beyond.
Enter the Quantum Weirdness
Quantum computing sounds like science fiction, and in many ways, it still is. But the core principles are real, and they’re genuinely strange. A quantum bit—a qubit—doesn’t have to be a zero or a one. It can be both simultaneously, in what’s called superposition. And multiple qubits can become “entangled,” linked in ways that transcend physical distance, sharing information instantaneously in what Einstein famously called “spooky action at a distance.”
These aren’t just interesting physics facts. They’re computational superpowers. Superposition allows quantum computers to explore multiple solutions simultaneously. Entanglement allows for correlations that classical systems simply cannot achieve. Together, they enable processing of complex, high-dimensional data in ways that would take classical computers millennia to accomplish.
But here’s where it gets interesting for those of us who care about building better systems: quantum mechanics might offer a way to do distributed AI that’s fundamentally more private and more efficient than anything classical computing can achieve.
The Breakthrough: Making It Work in the Real World
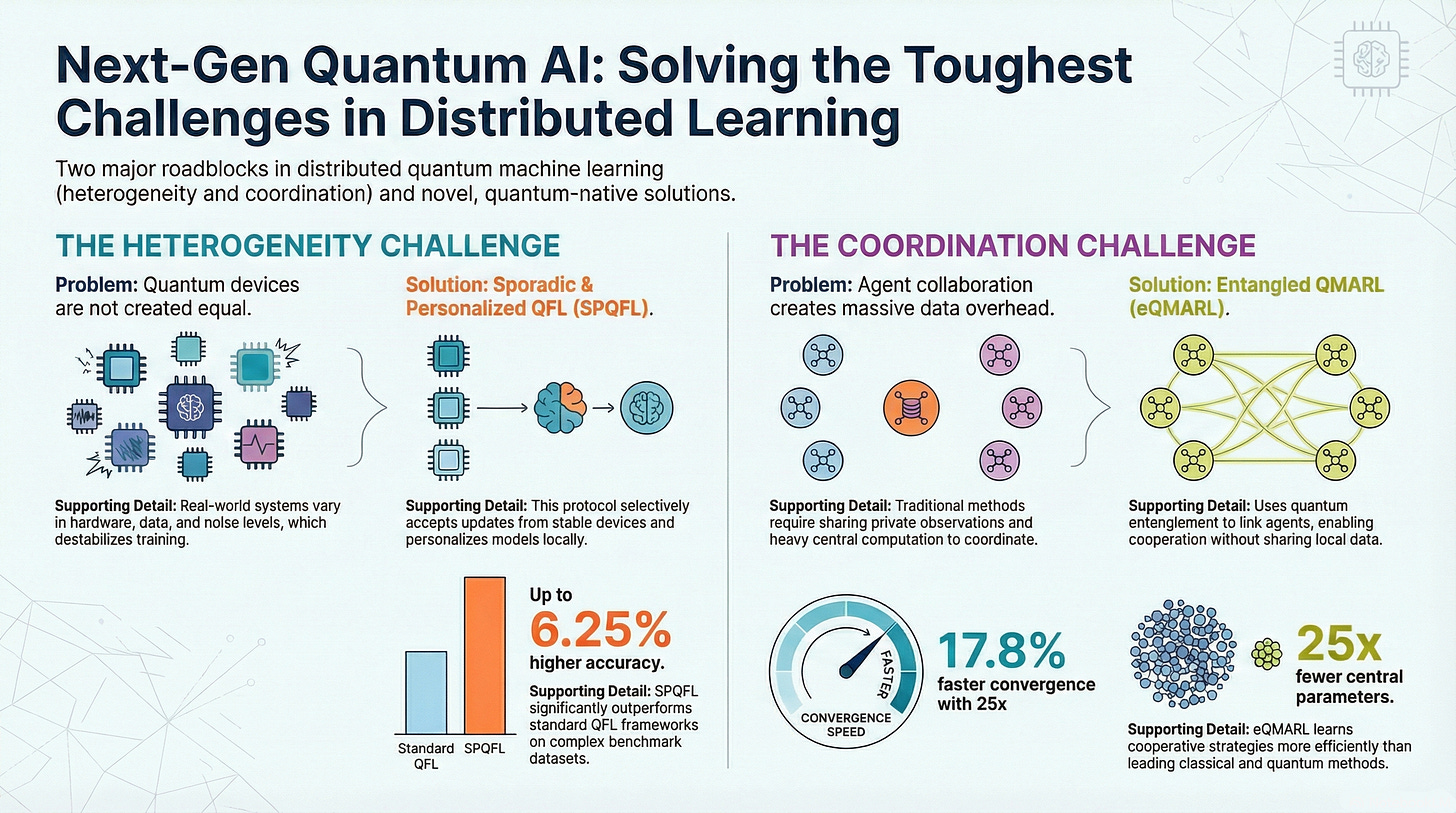
The researchers confronted a problem that most quantum computing work conveniently ignores: the real world is messy. Devices are different. Data is inconsistent. Quantum systems are incredibly fragile and prone to noise. The theoretical elegance of quantum algorithms falls apart when you try to deploy them across a network of diverse, imperfect devices.
This messiness—what they call “heterogeneity”—isn’t just a statistical problem. It’s a physics problem. When quantum states differ between devices, you can’t just average them like you would with classical data. They exist in incompatible mathematical spaces. It’s like trying to average the color red with the concept of justice—they’re fundamentally different kinds of information.
The solution they developed, called Sporadic Personalized Quantum Federated Learning (SPQFL), is elegant in its pragmatism. Instead of trying to force all devices to be identical, it accepts their differences and manages them intelligently. It allows devices to personalize their models for their local data while preventing them from drifting too far from the collective goal. And critically, it includes a quality gate: only devices that meet a certain performance threshold are allowed to contribute to the global model. Noisy, unreliable updates are filtered out automatically.
This isn’t just technical cleverness. It’s a different philosophy of collaboration—one that acknowledges diversity, manages differences, and maintains quality without centralized control.
From Infrastructure to Coordination: The Entanglement Revolution
But the really mind-bending innovation comes in how these researchers used quantum entanglement itself as a coordination mechanism for multi-agent AI systems.
Think about how robots or AI agents typically coordinate. They talk to each other. They share information. They send messages back and forth, consuming bandwidth, revealing their observations, and requiring a central coordinator to make sense of it all. It’s chatty, inefficient, and privacy-invasive.
The EQMRL (Entangled Quantum Multi-Agent Reinforcement Learning) framework does something radically different. Instead of having agents communicate explicitly, it uses quantum entanglement to create an implicit coordination channel. The agents’ decision-making processes are quantum-mechanically linked from the start. When one agent processes its local observation, that operation instantaneously influences the quantum state of the other agents—without any information being explicitly transmitted.
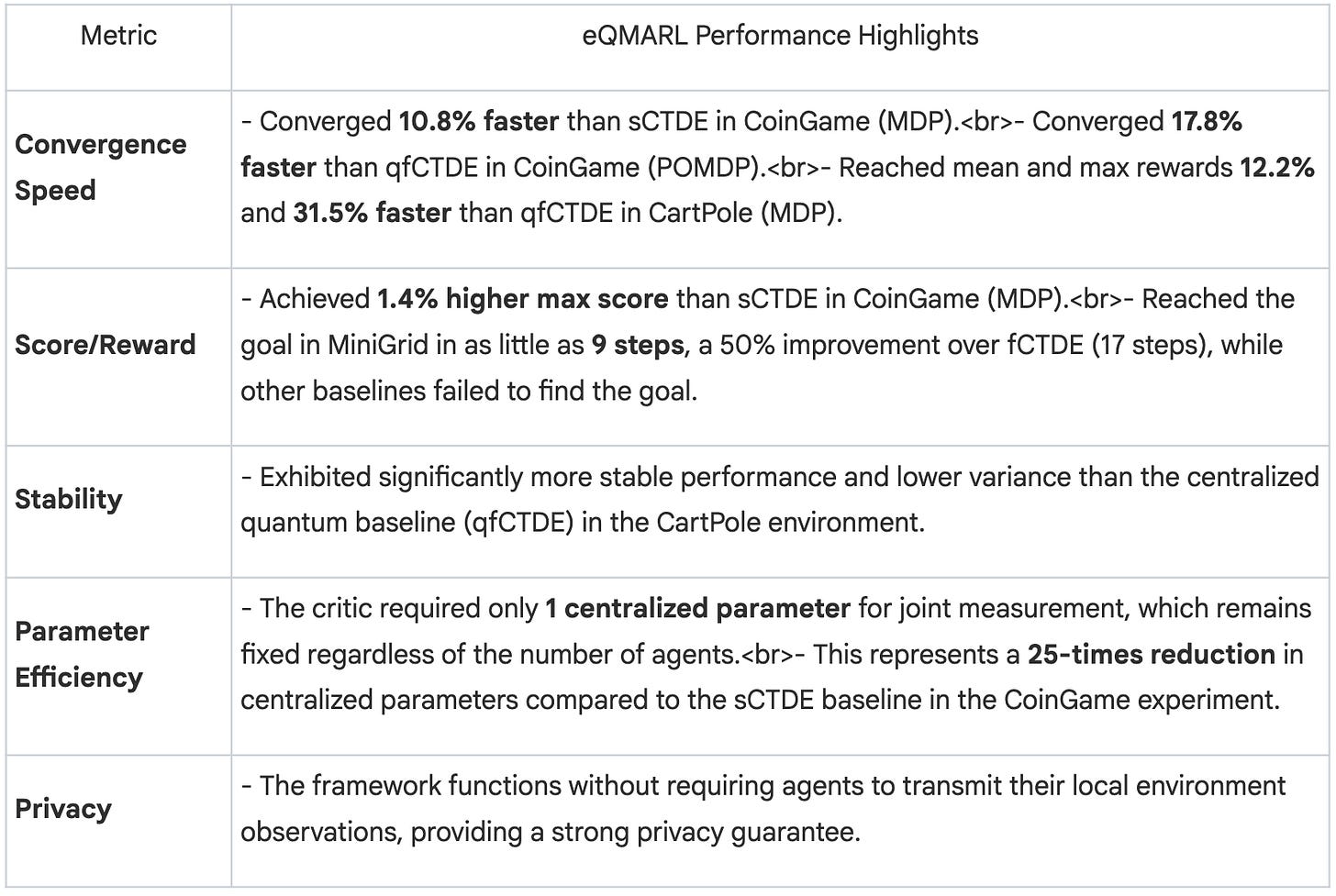
The results are striking. In benchmark tests, this entanglement-based coordination achieved 17.8% faster learning, better stability, and—here’s the kicker—required 25 times fewer parameters in the central server compared to classical approaches. That 25x reduction isn’t just an efficiency gain. It’s a fundamental shift in how the complexity of coordination scales as you add more agents.
What This Actually Means
Let me be clear: we’re not getting quantum-powered AI assistants next year. The technology is still in the research phase. The hardware is expensive, fragile, and limited. There are enormous engineering challenges ahead.
But the implications are worth considering. What these researchers have demonstrated is that it’s possible to build distributed AI systems that:
Keep your data local and private by design, not as an afterthought
Scale efficiently without requiring massive centralized infrastructure
Coordinate implicitly through quantum physics rather than explicit communication
Maintain quality through intelligent filtering rather than authoritarian control
This is a different vision of how AI could work. Not massive data centers owned by tech monopolies, but distributed networks where intelligence emerges from collaboration without coercion. Not surveillance machines that require you to surrender your privacy for convenience, but systems designed from the ground up to protect it.
The Bigger Picture
Margaret Atwood once wrote, “In the spring, at the end of the day, you should smell like dirt.” She was talking about gardening, about the importance of being grounded in the physical world even as our minds soar into abstraction. There’s wisdom there for how we think about technology.
We’ve spent decades building increasingly abstract, centralized, disembodied systems. The cloud. The algorithm. The platform. These metaphors distance us from the physical reality of what we’re creating—massive data centers consuming entire power plants’ worth of electricity, surveillance systems that would make dystopian novelists blush, attention-extraction mechanisms optimized to exploit our psychological vulnerabilities.
What’s interesting about this quantum AI research is that it forces us back to physics. You can’t ignore the physical reality of quantum systems—their fragility, their noise, their need for extreme cooling and isolation. You can’t pretend hardware doesn’t matter. You can’t centralize everything when quantum states decohere if you look at them wrong.
This physical constraint becomes a design principle. The limitations of quantum systems force a different architecture—distributed, privacy-preserving, accepting of diversity. The physics guides the ethics, in a sense.
Doris Lessing wrote about the importance of holding multiple contradictory truths simultaneously, of resisting simplistic narratives. The quantum revolution in AI embodies this. It’s both incredibly powerful and incredibly fragile. It’s both cutting-edge theoretical physics and pragmatic engineering. It’s both a breakthrough and a beginning, with enormous challenges still ahead.
What Comes Next
The researchers themselves outline the questions that define the next decade: How do you scale these systems to thousands or millions of devices? How do you manage aggregate errors in federated training loops? How do you guarantee stability when quantum connections are inherently fragile?
These aren’t just technical questions. They’re questions about what kind of technological future we want to build. Do we double down on centralization, surveillance, and control? Or do we explore architectures that distribute power, preserve privacy, and embrace diversity?
The quantum approach won’t solve everything. No technology does. But it offers a proof of concept that different approaches are possible. That intelligence doesn’t require surveillance. That coordination doesn’t require centralization. That we can build systems that work with physics rather than trying to dominate it.
In a world of increasingly dark technological news—algorithmic discrimination, surveillance capitalism, AI-powered misinformation—it’s rare to find research that offers genuine hope. Not the naive hope of techno-optimism, which assumes all innovation is good. But the grounded hope of seeing smart people working on hard problems with both technical sophistication and ethical awareness.
We won’t know for years whether quantum AI fulfills its promise. But the direction matters. And right now, at least some researchers are pointing toward a future where our machines might be both more powerful and more respectful of our humanity.
That’s worth paying attention to.
Link References
eQMARL: Entangled Quantum Multi-Agent Reinforcement Learning for Distributed Cooperation over Quantum Channels, arXiv (2024).
Towards Heterogeneous Quantum Federated Learning:
Challenges and Solutions. 2025
Episode Links
Available for broadcast on PRX
Other Links to Heliox Podcast
YouTube
Substack
Podcast Providers
Spotify
Apple Podcasts
Patreon
FaceBook Group
STUDY MATERIALS
Briefing
Executive Summary
This document synthesizes key findings from two seminal papers advancing the field of distributed quantum machine learning. The research addresses two critical, complementary challenges: achieving robustness in heterogeneous environments and leveraging quantum-native phenomena for efficient collaboration.
The first paper, “Towards Heterogeneous Quantum Federated Learning,” confronts the practical limitations of current Quantum Federated Learning (QFL) frameworks. It argues that the common assumption of client homogeneity is unrealistic and that real-world variances in data distributions, hardware capabilities, and quantum noise levels significantly degrade model performance and stability. The authors systematically categorize these variances into data heterogeneity and system heterogeneity, providing an in-depth analysis of their unique impacts in the quantum domain. To counter these issues, a comprehensive suite of mitigation strategies is proposed, alongside a case study on a Sporadic Personalized QFL (SPQFL) protocol. SPQFL demonstrates significant performance gains by selectively aggregating updates from reliable clients and personalizing models, proving the viability of robust learning in non-ideal quantum networks.
The second paper, “Entangled Quantum Multi-Agent Reinforcement Learning,” introduces a novel paradigm for cooperation in Quantum Multi-Agent Reinforcement Learning (QMARL). It posits that existing QMARL frameworks underutilize quantum mechanics by relying on classical communication for agent coordination. The proposed Entangled QMARL (eQMARL) framework pioneers the use of quantum entanglement as a primary medium for collaboration. By deploying a quantum entangled split critic, the framework couples decentralized agents over a quantum channel, eliminating the need to share private local observations. This approach not only enhances privacy but also drastically reduces classical communication overhead and centralized computational load. Experimental results show that eQMARL converges up to 17.8% faster than state-of-the-art baselines and operates with 25 times fewer centralized parameters, establishing entanglement as a powerful resource for efficient, decentralized cooperation.
Together, these works chart a course toward more practical and powerful distributed quantum intelligence. The first focuses on building resilience against the inevitable imperfections of near-term quantum systems, while the second pioneers a new, fundamentally quantum approach to multi-agent coordination, showcasing pathways to superior performance and efficiency.
--------------------------------------------------------------------------------
Part 1: Addressing Heterogeneity in Quantum Federated Learning (QFL)
Quantum Federated Learning (QFL) merges the privacy-preserving, decentralized training of federated learning with the computational power of quantum computing. However, its practical deployment is hindered by the inherent variability—or heterogeneity—among quantum clients, a challenge largely ignored by existing frameworks.
The Central Challenge of Heterogeneity
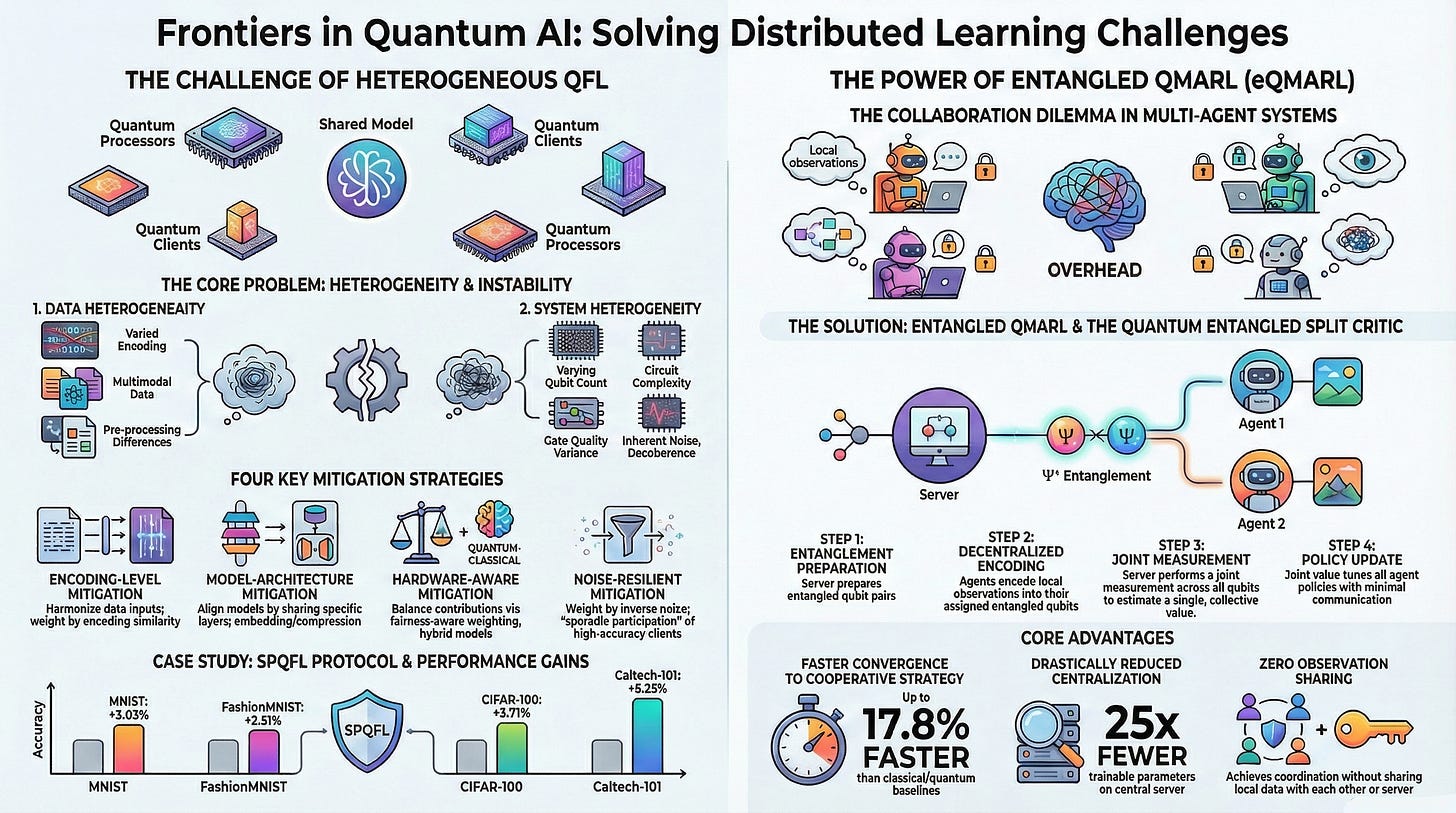
Current QFL models often assume that all participating clients are homogeneous, possessing identical quantum hardware, data distributions, and noise characteristics. This assumption breaks down in real-world scenarios, where variances can lead to training instability, slow convergence, and suboptimal model performance. The research identifies and classifies these variances into two primary categories.
1. Data Heterogeneity
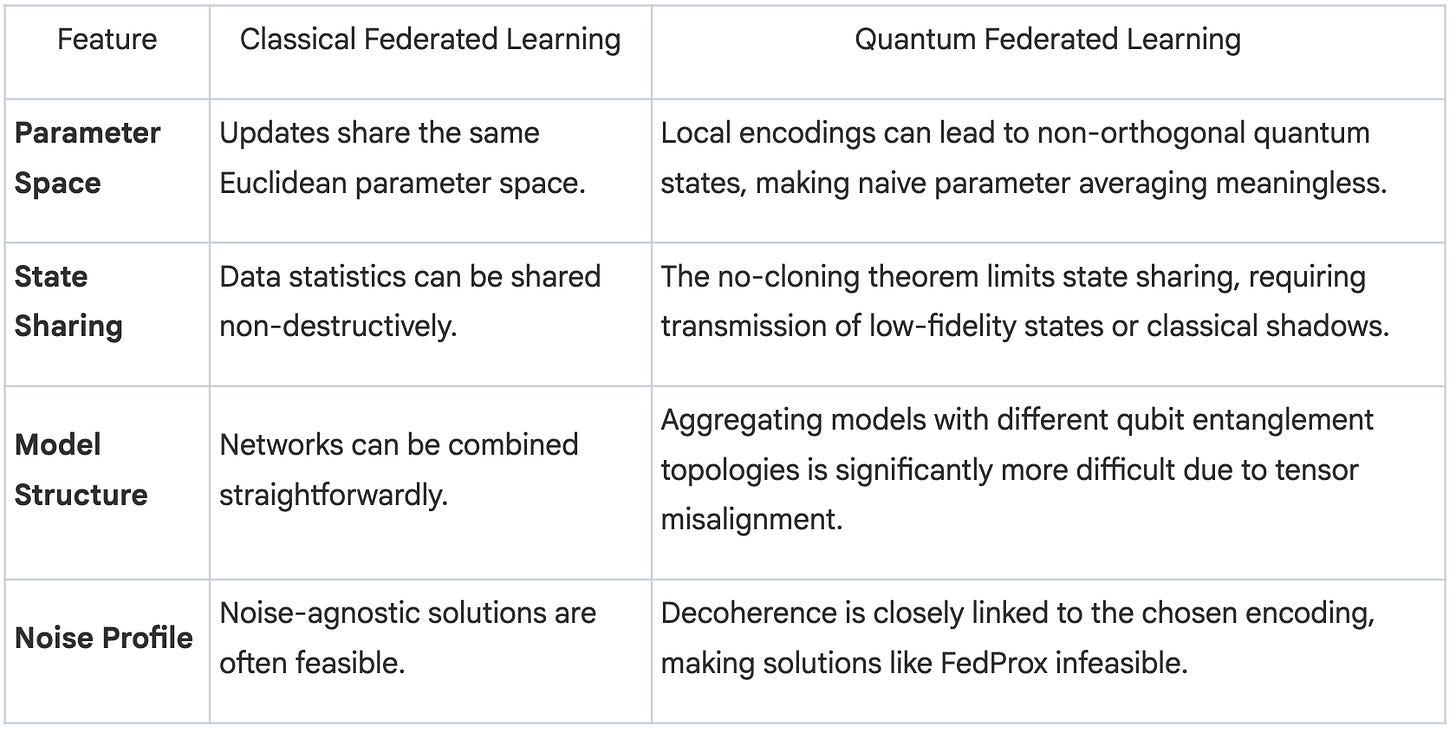
Data heterogeneity in QFL refers to differences in the quantum data representations across clients. This is a more complex issue than in classical federated learning (FL) because it is rooted in the physics of quantum mechanics.
• Classical vs. Quantum Data Heterogeneity: In classical FL, heterogeneity typically involves non-IID data distributions, but all clients operate within a shared Euclidean parameter space. In QFL, the challenges are more fundamental:
◦ Incompatible Bases: Different local encoding methods can map identical classical data to non-orthogonal quantum states, making a naive averaging of parameters theoretically meaningless.
◦ No-Cloning Theorem: This quantum principle prevents the simple sharing of an acquired quantum state, forcing clients to transmit either low-fidelity states or classical summaries, which introduces representation-dependent noise.
◦ Entanglement Mismatch: Different Parameterized Quantum Circuits (PQCs) can entangle qubits according to their unique topology, complicating the aggregation of models that act on different tensor-product factors.
◦ Encoding-Dependent Noise: Decoherence is closely linked to the chosen encoding scheme (amplitude, phase, or basis), making noise-agnostic solutions from classical FL ineffective.
• Sources of Data Heterogeneity:
◦ Heterogeneous Quantum Encoding: Clients may use different methods (basis, amplitude, phase, entanglement) or variations in pre-processing and normalization, leading to inconsistent quantum state representations and divergent feature spaces.
◦ Multimodal Data: Clients may process a mix of data types (quantum states, classical text, images), leading to uneven contributions to the global model and challenges in data fusion and integration. This can skew the global model toward data-rich modalities.
2. System Heterogeneity
System heterogeneity concerns the physical and architectural variances in the quantum hardware used by different clients.
• Heterogeneous PQC Architecture: Clients with varying hardware resources (qubit count, coherence times, gate quality) may employ PQCs of different depths and complexity. This mismatch complicates global aggregation, as parameters from circuits with different expressive capacities do not map directly. It also raises fairness issues, as clients with simpler circuits may contribute less significant updates.
• Varying Qubit Counts: Differences in available qubits directly limit a client’s computational power and its ability to represent complex, high-dimensional data. This can create inconsistencies in parameter size and state dimensions, increasing communication overhead.
• Inherent Quantum Noise: Quantum devices experience unique noise patterns, causing local model updates to be inconsistent. Key sources include:
◦ Decoherence: The loss of quantum state due to environmental interaction varies based on hardware quality, causing clients with higher decoherence to provide noisier, less reliable updates.
◦ Gate Noise: Imperfections in quantum gate operations lead to varying fidelities across devices. Clients with lower fidelity contribute error-prone updates, degrading global model performance.
Mitigation Strategies for Heterogeneous QFL
To combat the effects of heterogeneity, the research proposes a four-pronged approach to mitigation.
ase Study: Sporadic Personalized QFL (SPQFL)
A case study featuring the Sporadic Personalized Quantum Federated Learning (SPQFL) protocol demonstrates the practical application of these mitigation principles. SPQFL is designed to jointly tackle quantum noise and non-IID data distributions.
• Core Mechanisms:
1. Sporadic Learning: Before aggregation, each client’s local model is evaluated. Only models that achieve a validation accuracy above a predefined threshold (τ) are sent to the server. This selective participation filters out noisy or suboptimal updates.
2. Personalization: The local update rule includes a regularization term that balances the local model’s parameters with the global model’s parameters, allowing each client to adapt to its unique data while remaining aligned with the collective goal.
• Architecture Overview: As illustrated in the SPQFL architecture diagram, distributed quantum clients train local Quantum Neural Network (QNN) models. These models use PQCs to process encoded data. The updated parameters (ωn,k) are then selectively sent to a central quantum server for global aggregation.
• Performance: SPQFL was benchmarked against state-of-the-art methods (QNN, QCNN, QFL, PQFL, wpQFL) across four datasets (MNIST, Fashion-MNIST, CIFAR-100, Caltech-101).
◦ The results show that SPQFL consistently outperforms existing approaches in both accuracy and convergence speed.
◦ Compared to a standard QFL baseline, SPQFL improved accuracy by 3.03% on MNIST, 2.51% on Fashion-MNIST, 3.71% on CIFAR-100, and 6.25% on Caltech-101.
◦ It also achieved a 1.6% accuracy improvement over the personalized QFL (PQFL) approach across all datasets.
--------------------------------------------------------------------------------
Part 2: Entanglement for Cooperation in Quantum Multi-Agent Reinforcement Learning (QMARL)
While QFL focuses on collaborative model training, Quantum Multi-Agent Reinforcement Learning (QMARL) applies quantum principles to decision-making in decentralized, multi-agent environments. A key challenge in QMARL is fostering cooperation among agents, which has historically relied on classical communication channels for sharing information. The eQMARL framework proposes a paradigm shift, using quantum entanglement as a direct medium for coordination.
The eQMARL Framework
The Entangled QMARL (eQMARL) framework is a novel distributed actor-critic architecture that lies at the intersection of centralized training and decentralized execution. It is designed to facilitate agent collaboration over a quantum channel, thereby eliminating the need for agents to share their local environment observations.
• Core Innovation: The Entangled Split Critic: The central component of eQMARL is a quantum critic network that is “split” across all participating agents. Each agent hosts a local branch of the critic, implemented as a Variational Quantum Circuit (VQC). These distributed branches are intrinsically linked via quantum entanglement.
• Architectural Workflow:
1. Input State Entanglement: A trusted central server prepares sets of entangled qubits. The specific type of entanglement (e.g., Bell states) is a key design choice. These entangled qubits are then distributed to the agents via a quantum channel.
2. Decentralized Observation Encoding: Each agent receives its local observation from the environment and encodes this classical information into its assigned (and already entangled) qubits using its local VQC branch. The parameters of this VQC are tuned locally.
3. Centralized Joint Measurement: The agents transmit their processed qubits back to the central server. The server performs a joint quantum measurement across all qubits from all agents simultaneously. This measurement yields a single joint value, which estimates the collective “goodness” of the agents’ current policies. This value is used to calculate a critic loss.
4. Decentralized Policy Update: The server computes a partial gradient of the loss and transmits this small amount of classical information back to the agents, who then update their local critic and actor (policy) networks.
This design minimizes classical communication to just rewards and a single partial gradient value. It also drastically reduces the computational load on the central server, whose only trainable parameter is a single scaling factor for the joint measurement.
The Role and Impact of Entanglement
Entanglement serves as the cooperative backbone of the eQMARL framework, coupling the agents’ local critic branches without any explicit exchange of local data.
• Comparative Analysis of Entanglement Styles: The framework was tested with four different types of two-qubit Bell state entanglement: Φ+, Φ−, Ψ+, and Ψ−.
◦ Experiments on the CoinGame environment revealed that Ψ+ entanglement consistently delivered the best performance, achieving faster convergence and higher final scores in both fully observable (MDP) and partially observable (POMDP) settings.
◦ In the POMDP setting, Ψ+ achieved a score threshold of 25 10.7% faster than the next-best non-entangled approach. The poorer performance of Φ+ and Φ− suggests that opposite-state entanglement (|01⟩ and |10⟩) provides a more effective coupling mechanism than same-state entanglement (|00⟩ and |11⟩) for this task.
• Implicit Collaboration: By entangling the input qubits, the local encoding process of one agent influences the joint measurement outcome in a way that is correlated with the actions of all other agents. This creates an implicit coordination channel that allows agents to learn a cooperative strategy without ever seeing each other’s observations.
Performance and Efficiency Gains
eQMARL was benchmarked against three state-of-the-art baselines: a fully centralized classical critic (fCTDE), a split classical critic (sCTDE), and a fully centralized quantum critic (qfCTDE). The experiments were conducted across three distinct multi-agent environments: CoinGame, CartPole, and MiniGrid.
--------------------------------------------------------------------------------
Conclusion and Future Directions
The research detailed in this briefing marks significant progress toward realizing practical, large-scale distributed quantum machine learning systems. By tackling the distinct but related challenges of heterogeneity and inter-agent cooperation, these studies provide both foundational robustness and a vision for advanced, quantum-native functionality.
• The work on heterogeneous QFL establishes a clear framework for understanding and mitigating the real-world variances that plague near-term quantum devices. The proposed mitigation strategies and the success of the SPQFL protocol offer a tangible pathway to building QFL systems that are resilient to noise, hardware differences, and data imbalances.
• The eQMARL framework represents a paradigm shift in multi-agent learning, demonstrating for the first time that quantum entanglement can be harnessed as a powerful and efficient resource for coordination. By eliminating the need for observation sharing and minimizing classical communication, eQMARL offers a scalable, private, and high-performing solution for complex cooperative tasks.
Several open research topics emerge from these findings, highlighting the next frontiers for the field:
• Scalability and Robustness: Future work must develop more adaptable and noise-resilient algorithms that can scale to large quantum networks while maintaining efficiency, privacy, and performance.
• Advanced Error Mitigation: Integrating advanced quantum error correction codes and error-aware learning algorithms directly into distributed frameworks is crucial for mitigating not only hardware-level noise but also aggregate errors that arise during federated training.
• Quantum Network Dynamics: Research is needed to understand how unique quantum network phenomena—such as decoherence-induced latency and entanglement generation failures—affect the stability and performance of distributed learning systems.
• Hardware and Simulation Overheads: The computational complexity of simulating large quantum systems on classical hardware remains a bottleneck. Continued progress in both quantum hardware and simulation techniques is essential for validating these frameworks at scale.
Quiz & Answer Key
Answer each of the following questions in 2-3 sentences based on the provided source context.
1. What is Quantum Federated Learning (QFL), and what primary challenge does it aim to solve compared to conventional Quantum Machine Learning (QML)?
2. The “Towards Heterogeneous QFL” paper divides heterogeneity into two main categories. What are they, and what does each one generally refer to?
3. Explain the concept of a split quantum critic as implemented in the eQMARL framework. How does it facilitate cooperation between agents?
4. What is inherent quantum noise in QFL systems, and what are its three primary sources mentioned in the text?
5. How does the eQMARL framework reduce classical communication overhead and centralized computational burden compared to baseline models?
6. According to the SPQFL case study, what two design choices contribute to its superior performance in accuracy and convergence speed?
7. What is the fundamental difference between data heterogeneity in classical Federated Learning (FL) and Quantum Federated Learning (QFL)?
8. In the eQMARL experiments, which Bell state entanglement scheme generally resulted in better performance, and what does this suggest about the effectiveness of same-state versus opposite-state entanglement?
9. Describe the “Sporadic Participation” mitigation strategy for noise-resilient QFL. How does it work to minimize error propagation?
10. What is a Variational Quantum Circuit (VQC), and what are its main components as described in the eQMARL paper?
--------------------------------------------------------------------------------
Answer Key
1. What is Quantum Federated Learning (QFL), and what primary challenge does it aim to solve compared to conventional Quantum Machine Learning (QML)? Quantum Federated Learning (QFL) is a machine learning approach that combines quantum computing with federated learning to perform tasks across distributed networks. It addresses the significant privacy concerns and high communications overhead of conventional QML, where data is typically collected and processed on a central server. By training models locally on distributed quantum devices and aggregating only the model parameters, QFL maintains data privacy and reduces data transfer needs.
2. The “Towards Heterogeneous QFL” paper divides heterogeneity into two main categories. What are they, and what does each one generally refer to? The two categories are data heterogeneity and system heterogeneity. Data heterogeneity refers to differences in the representations of quantum data between clients, such as variations in quantum encoding methods or data distributions. System heterogeneity refers to variances in the quantum hardware between clients, including differences in qubit count, noise levels, coherence times, and gate fidelities.
3. Explain the concept of a split quantum critic as implemented in the eQMARL framework. How does it facilitate cooperation between agents? The split quantum critic in eQMARL is a joint value function estimator that is spread across multiple agents as a split neural network, with each agent’s local Variational Quantum Circuit (VQC) serving as a branch. It facilitates cooperation by coupling the agents’ localized observation encoders using entangled input qubits over a quantum channel. This allows agent policies to be tuned through joint value estimation via joint quantum measurements, eliminating the need for agents to explicitly share their local observations.
4. What is inherent quantum noise in QFL systems, and what are its three primary sources mentioned in the text? Inherent quantum noise is the collection of errors and irregularities that occur in quantum systems and vary between quantum devices, causing local model updates to become inconsistent. The three primary sources mentioned are decoherence, which is the loss of a quantum state due to environmental interactions; gate noise, caused by hardware faults and control imperfections during qubit calculations; and measurement irregularities.
5. How does the eQMARL framework reduce classical communication overhead and centralized computational burden compared to baseline models? The eQMARL framework reduces classical communication overhead by using a quantum channel and entanglement to couple agents, eliminating the need to send local environment observations or intermediate neural network activations over classical channels. It reduces the centralized computational burden because the joint value is estimated via a joint quantum measurement that relies on only a single learned scaling parameter on the central server, which remains fixed regardless of the number of agents.
6. According to the SPQFL case study, what two design choices contribute to its superior performance in accuracy and convergence speed? The two key design choices are a regularization-based approach and a sporadic (occasional) learning mechanism. The regularization penalizes overfitting in local quantum circuits and stabilizes training for heterogeneous clients. The sporadic learning mechanism prevents noisy or sub-par updates from corrupting the global model by only allowing local models to be sent to the server if their validation accuracy is above a predetermined threshold.
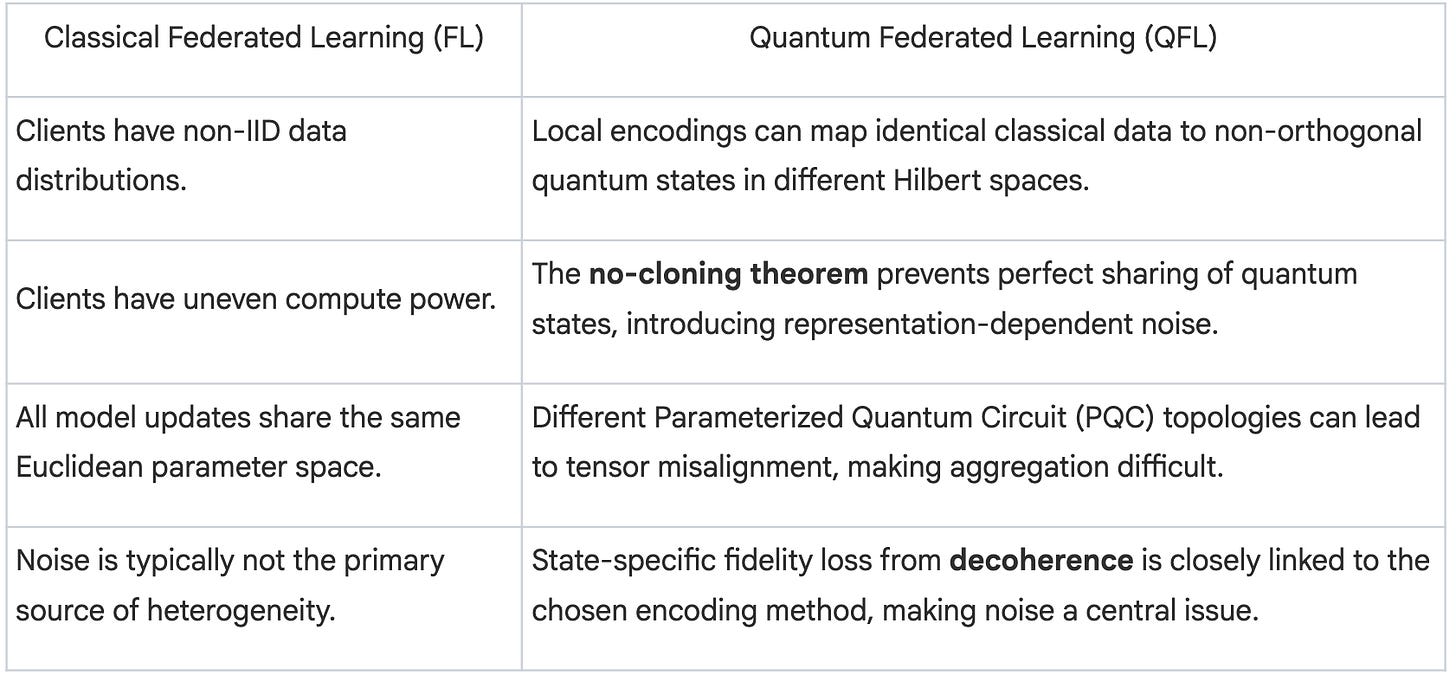
7. What is the fundamental difference between data heterogeneity in classical Federated Learning (FL) and Quantum Federated Learning (QFL)? In classical FL, clients have non-IID data but all model updates share the same Euclidean parameter space. In contrast, data heterogeneity in QFL stems from the physics of Hilbert space, where local encodings can convert identical classical data into non-orthogonal quantum states, making a naive parameter average theoretically meaningless. Additionally, QFL heterogeneity is affected by quantum-specific issues like the no-cloning theorem, representation-dependent noise, and decoherence linked to the encoding method.
8. In the eQMARL experiments, which Bell state entanglement scheme generally resulted in better performance, and what does this suggest about the effectiveness of same-state versus opposite-state entanglement? The Ψ+ entanglement scheme consistently demonstrated the best performance across both MDP and POMDP dynamics in the CoinGame environment. The superior performance of Ψ+ (an opposite-state entanglement of |01⟩ and |10⟩) compared to the poorer performance of Φ+ and Φ- (same-state entanglements of |00⟩ and |11⟩) suggests that opposite-state entanglement results in more effective coupling of agents.
9. Describe the “Sporadic Participation” mitigation strategy for noise-resilient QFL. How does it work to minimize error propagation? Sporadic participation is a strategy where only clients that fulfill a specific validation criterion, such as local accuracy meeting a threshold τ, are permitted to join the aggregation round. This adaptive participation prevents unstable updates from clients experiencing noise spikes from being included in the global model. By filtering out unreliable contributions, this method minimizes error propagation throughout the QFL system.
10. What is a Variational Quantum Circuit (VQC), and what are its main components as described in the eQMARL paper? A Variational Quantum Circuit (VQC) is a hybrid quantum-classical model used as a branch of the split critic in the eQMARL framework. As described, it consists of L cascaded layers, each containing three main operator components: a trainable variational layer for parameterized Pauli-axis rotations, a non-trainable circular entanglement layer to bind neighboring qubits, and a trainable encoding layer to map classical features into a quantum state.
Essay Questions
Answer the following questions in a detailed essay format, drawing upon the comprehensive information provided in the source context. No answers are provided for this section.
1. Discuss the concept of heterogeneity in Quantum Federated Learning (QFL) as presented in the source material. Contrast the challenges of data heterogeneity and system heterogeneity, providing specific examples for each, and explain why mitigation strategies from classical FL are often inadequate.
2. Detail the architecture and workflow of the proposed Entangled QMARL (eQMARL) framework. Your explanation should cover the roles of the central server and decentralized agents, the process of joint input entanglement, the design of the decentralized split critic, and the function of centralized joint measurement.
3. The “Towards Heterogeneous QFL” paper outlines four categories of mitigation strategies. Choose two of these categories (Encoding-Level, Model-Architecture, Hardware-Aware, Noise-Resilient), and for each, describe two specific techniques mentioned in the text, including any mathematical formulas provided.
4. Analyze the experimental results from the eQMARL paper’s CoinGame experiments. Compare the performance of eQMARL-Ψ+ against the classical (fCTDE, sCTDE) and quantum (qfCTDE) baselines in both MDP and POMDP settings, focusing on convergence speed and overall score. What do these results imply about the “quantum advantage” in this context?
5. Based on the “Conclusion and Open Research Topics” section of the QFL paper, identify and elaborate on the three key open research areas for improving heterogeneous QFL frameworks. For each area, explain the core problem and the direction future research should take.
Glossary of Key Terms
Actor-Critic Architecture
A popular approach in multi-agent reinforcement learning that tunes policies (actors) using an estimator that evaluates how good or bad the policy is at any given state (the critic).
Amplitude Encoding
A method of quantum encoding that represents classical data in the amplitudes of quantum states for compact storage.
Bell States
A set of four specific, maximally entangled two-qubit quantum states ({
Centralized Training with Decentralized Execution (CTDE)
A multi-agent reinforcement learning framework where decentralized agent policies learn using a joint value function at training time, often deployed on a central server, while agents interact with the environment independently during execution.
Data Heterogeneity (in QFL)
Refers to differences in the representations of quantum data between clients in a QFL network. This can arise from different quantum encoding techniques, data distributions, or hardware variations affecting data processing.
Decoherence
A process in quantum systems where qubits lose their quantum state (superposition or entanglement) as a result of environmental interactions. It is a primary source of inherent quantum noise.
Entangled QMARL (eQMARL)
A novel, distributed actor-critic framework for QMARL that facilitates agent collaboration over a quantum channel. It uses a quantum entangled split critic to eliminate local observation sharing and reduce classical communication overhead.
Entanglement
A quantum mechanical property where the states of two or more qubits become intrinsically linked, regardless of their physical separation. If a combined quantum system’s state cannot be separated into a tensor product of its individual components, it is said to be entangled.
Federated Averaging (FedAvg)
A method used in federated learning for model aggregation where trainable parameters from local models are extracted, translated to classical data, and averaged to create an updated global model.
Gate Noise
A source of quantum noise introduced by hardware faults, control imperfections, and external interference during the operation of quantum gates on qubits.
Heterogeneity (in QFL)
The inherent variability that exists in real-world quantum systems, which is classified into two types: data heterogeneity (variances in quantum data distributions and encoding) and system heterogeneity (variances in quantum hardware).
Inherent Quantum Noise
Errors that occur in quantum systems due to quantum decoherence, gate noise, and measurement irregularities, which vary between quantum devices and make local model updates inconsistent.
Joint Quantum Measurement
A process in eQMARL where a centralized server performs a measurement across all qubits from all agents in the system simultaneously. This is used to estimate a joint value for the locally-encoded observations.
Markov Decision Process (MDP)
A mathematical framework for modeling decision-making in environments with full information, where an agent’s observations represent the complete state of the environment.
Noisy Intermediate-Scale Quantum (NISQ) Devices
The current generation of distributed quantum devices which have a limited number of qubits and are susceptible to decoherence and other forms of noise.
Parameterized Quantum Circuit (PQC)
A quantum model comprised of quantum gates controlled by adjustable parameters, typically implemented as rotations. By altering these parameters, PQCs can process data, explore Hilbert spaces, and extract patterns.
Partially Observable Markov Decision Process (POMDP)
A mathematical framework for modeling decision-making in environments with partial information, where the full state is hidden and agents receive local observations that may not represent the complete environment state.
Pauli Gates (X, Y, Z)
A set of fundamental single-qubit quantum gates. The Pauli-X gate is a quantum variant of the NOT gate, and all three are used in parameterized rotations (RX, RY, RZ).
Quantum Bit (Qubit)
The fundamental unit of quantum computation. A qubit can exist in a superposition of 0 and 1 simultaneously, and its state is represented as a 2-dimensional unit vector in a complex Hilbert space.
Quantum Channel
A communication channel that allows for the direct transfer of quantum states, for example through quantum teleportation. This preserves quantum coherence but requires consistent entanglement distribution and high-fidelity connections.
Quantum Encoding
The process of transforming classical data into quantum states using quantum gates for computation. Common methods include basis, amplitude, phase, and entanglement encoding.
Quantum Federated Learning (QFL)
An approach that combines quantum computing with federated learning to perform machine learning tasks across distributed networks, enabling decentralized model training while maintaining data privacy.
Quantum Gate
The basic reversible operations that alter the states of qubits. Examples include Pauli-X, Hadamard (for superposition), and CNOT (for entanglement).
Quantum Machine Learning (QML)
A field that integrates quantum physics with machine learning techniques, leveraging quantum phenomena like superposition and entanglement to process complex data at high speeds.
Quantum Multi-Agent Reinforcement Learning (QMARL)
A variant of QRL that applies quantum computing to scenarios with multiple learning agents, with potential synergies between decentralized cooperation and quantum entanglement.
Quantum Neural Network (QNN)
A quantum model where quantum layers, often built with PQCs, replace classical layers to learn complex patterns.
Quantum Reinforcement Learning (QRL)
A class of quantum machine learning for decision-making that exploits the performance and data encoding enhancements of quantum computing.
Split Quantum Critic
A key component of the eQMARL framework, where a joint value function estimator (the critic) is implemented as a quantum split neural network. Each agent’s local VQC serves as a branch, and the branches are coupled via entangled input qubits over a quantum channel.
Sporadic Personalized Quantum Federated Learning (SPQFL)
A proposed QFL protocol designed to jointly tackle quantum noise and non-IID data distributions. It uses a sporadic participation mechanism and regularization-based personalization to improve model performance.
Superposition
A fundamental property of quantum mechanics where a quantum system, such as a qubit, can exist in a combination of multiple states (e.g., both 0 and 1) at the same time.
System Heterogeneity (in QFL)
Refers to variances in quantum hardware between clients, such as differences in qubit count, coherence times, error rates, and gate fidelities, impacting local training performance.
Variational Quantum Circuit (VQC)
A hybrid quantum-classical model that uses parameterized quantum gates optimized via classical methods like gradient descent. In the context of the provided sources, it is used to build quantum neural networks and the branches of the split critic.
Timeline of Main Events
The field of distributed quantum machine learning is not defined by a single breakthrough but by a continuous progression of evolving challenges and the innovative solutions developed to overcome them. Each solution, while powerful, tends to reveal a deeper, more complex problem lying beneath. This document traces this technological narrative, charting the course from the initial limitations of centralized Quantum Machine Learning (QML), through the intricate problems of hardware and data heterogeneity in Quantum Federated Learning (QFL), to the advanced complexities of fostering cooperation between intelligent quantum agents.
1. The Foundational Challenge: From Centralized QML to Distributed QFL
Quantum Machine Learning (QML) first emerged as a discipline of immense promise, leveraging quantum phenomena such as superposition and entanglement to process complex, large-scale data at unprecedented speeds. By integrating quantum physics with advanced machine learning, QML frameworks offered a new paradigm for computation. However, the conventional, centralized architecture of early QML models presented fundamental barriers to practical deployment.
These limitations effectively stalled the real-world application of QML in scenarios involving sensitive or continuous data processing. The primary problems were:
• Privacy Concerns: In most conventional QML frameworks, data must be collected and processed on a central server. This model raises significant privacy issues, exposing potentially sensitive information to various data-based attacks.
• Communication Overhead: The transfer of large-scale, high-dimensional data from distributed sources to a central processor creates substantial communication overhead. This bottleneck leads to slower overall performance and presents significant scalability challenges.
To address these foundational challenges, researchers developed Quantum Federated Learning (QFL). This promising approach redesigns the learning process, combining the principles of classical federated learning with the power of quantum computing. The core concept of QFL is to perform machine learning tasks across a distributed network of quantum devices, or “clients.” Each client trains a local model on its own data, and only the model parameters—not the raw data—are sent to a central server for aggregation. This method inherently protects data privacy and dramatically reduces communication overhead.
However, once the QFL framework solved the initial problems of privacy and data transfer, its practical implementation uncovered the next major hurdle on the technological timeline: the profound and multifaceted challenge of heterogeneity.
2. The First Major Hurdle: Deconstructing Heterogeneity in QFL
While QFL provided a robust architectural solution to the problems of centralized QML, its deployment in real-world networks revealed a critical new challenge: the inherent and significant differences between quantum clients. Understanding and mitigating this heterogeneity became strategically imperative for the field to advance.
The heterogeneity found in QFL is fundamentally different and far more complex than that in classical Federated Learning (FL). In classical FL, heterogeneity typically arises from non-identical data distributions or varied computational capacities among clients, but all model updates exist within a shared Euclidean parameter space. In contrast, QFL heterogeneity is rooted in the physics of quantum mechanics itself. Because local encodings can map identical classical data to non-orthogonal quantum states, updates from different clients may have incompatible bases in Hilbert space, rendering naïve parameter averaging mathematically meaningless. Furthermore, the no-cloning theorem prevents the perfect sharing of quantum states, forcing clients to transmit classical summaries and introducing representation-dependent noise with no classical equivalent. Aggregating models that act on various tensor-product factors is also significantly more difficult than combining classical networks.
To systematically address this, heterogeneity in QFL can be classified into two primary categories: data heterogeneity and system heterogeneity.
2.1 Data Heterogeneity: The Challenge of Inconsistent Representations
Data heterogeneity in QFL refers to the differences in how quantum data is represented and structured across clients. This makes it exceptionally difficult to align and aggregate local models into a cohesive global model. The primary sources of this challenge include:
1. Heterogeneous Quantum Encoding: Clients may use distinct methods to encode classical data into quantum states, such as basis, amplitude, or phase encoding. Even when clients use the same encoding strategy, differences in data pre-processing or normalization can result in inconsistent quantum state representations. This leads to divergent feature spaces, where local models learn different quantum representations from the same underlying data, complicating the creation of a globally consistent model.
2. Multimodal Data Across Devices: In many real-world scenarios, clients manage varied types of data, or modalities. This can include quantum states and measurement outcomes alongside classical inputs like text and images. This diversity complicates data integration, as modality-specific noise and formatting incompatibilities propagate during global training. Consequently, the global model can become skewed toward clients with richer or higher-quality data, impairing its ability to generalize and increasing both communication and computational costs.
2.2 System Heterogeneity: The Challenge of Hardware Variances
System heterogeneity refers to the physical variances in quantum hardware and computational capabilities among clients in a QFL network. These differences mean that clients cannot perform computations equally, leading to imbalances in training time, update accuracy, and operational capacity. Key sources include:
1. Heterogeneous PQC Architectures: Clients often use Parameterized Quantum Circuits (PQCs)—the quantum analog of neural network layers—with varying depths and structural complexity. These differences are typically dictated by hardware limitations, such as qubit availability, coherence times, and gate quality. A low-resource client may only support a shallow PQC, while a more advanced device can run a deeper, more expressive circuit. This mismatch hampers global aggregation, as parameters learned from circuits with different capacities do not map directly.
2. Varying Number of Qubits: The number of available qubits can differ significantly across client devices. Clients with fewer qubits have lower computational power and a more limited capacity to represent high-complexity data. This variance also creates communication overhead, as differing qubit counts lead to inconsistent parameter sizes and quantum state dimensions across the network.
3. Inherent Quantum Noise: Quantum processors are intrinsically noisy, and each device experiences unique noise patterns. This inconsistency means that local model updates from different clients are of varying quality. The main types of noise are:
◦ Decoherence: The loss of a quantum state due to interactions with the environment. Clients with higher decoherence rates contribute noisier and less reliable parameter updates, slowing global convergence.
◦ Gate Noise: Errors introduced by hardware faults and imperfections in the control of quantum gates. Variances in gate fidelities result in unequal local training quality.
◦ Measurement Irregularities: Discrepancies in the process of extracting classical results from a quantum system add another layer of inconsistency to the updates.
The formal identification and categorization of these heterogeneity challenges spurred the development of a range of targeted mitigation strategies designed to make QFL robust and practical.
3. Countermeasures: The Development of Mitigation Strategies for Heterogeneity
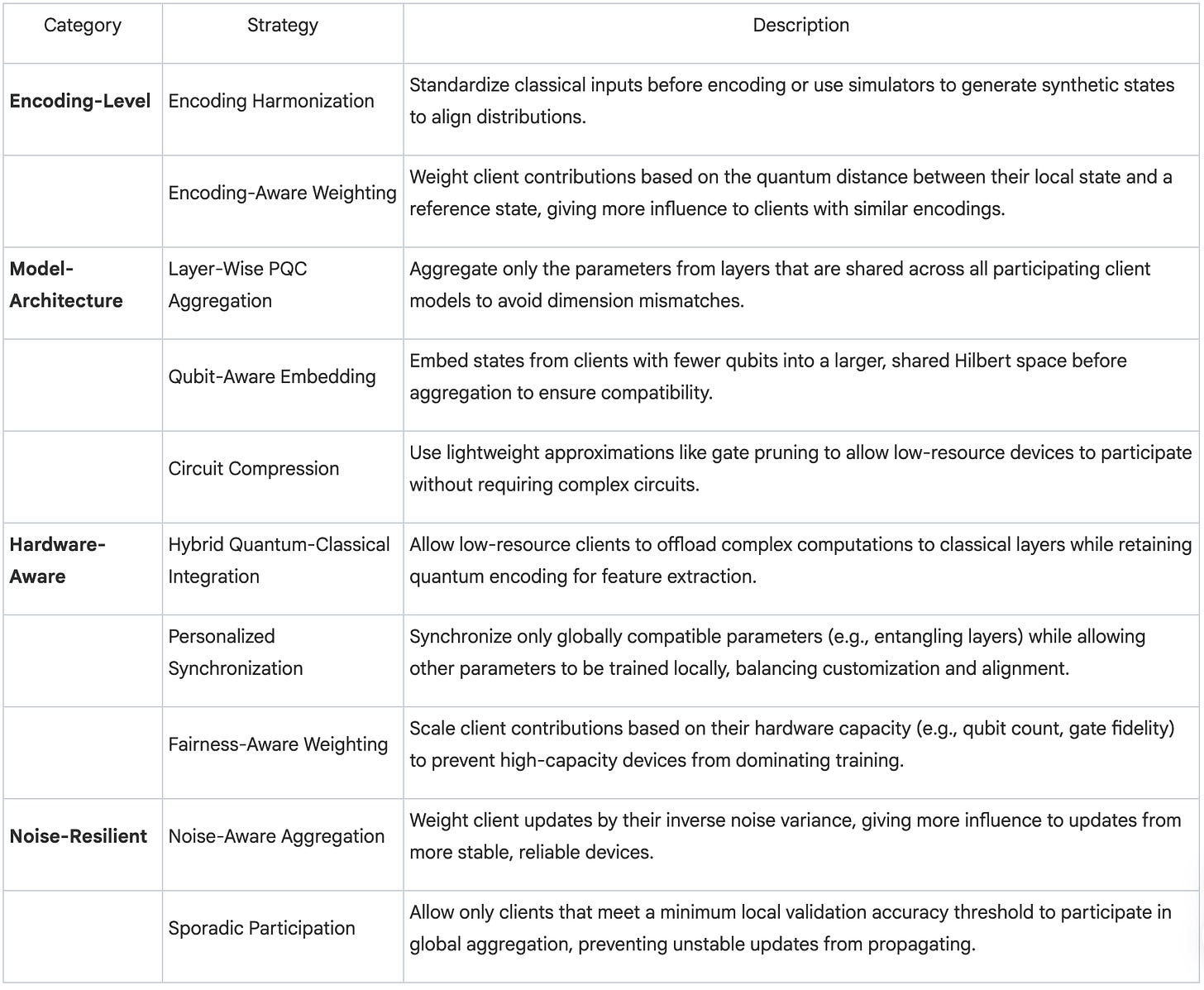
In response to the critical challenge of heterogeneity, researchers have developed a portfolio of mitigation strategies. These techniques are designed to create stability and fairness in QFL networks by intervening at different levels of the learning process, whether at the point of data encoding, within the model architecture, by accounting for hardware differences, or by building in resilience to quantum noise.
3.1 Encoding-Level Mitigations
These strategies address inconsistencies in how data is represented in quantum states.
• Encoding Harmonization: Standardizing classical inputs across all clients before they are encoded into quantum states to align data distributions.
• Encoding-Aware Weighting: Weighting client contributions during aggregation based on the similarity of their quantum state (ρi) to a global reference state (ρg), as measured by a quantum distance metric, d(·,·): wi = exp(−αd(ρi,ρg)) / ∑ exp(−αd(ρj,ρg)).
3.2 Model-Architecture Strategies
These techniques manage structural incompatibilities between the quantum models on different clients.
• Layer-Wise PQC Aggregation: Aggregating only the parameters (θli) from PQC layers shared by all clients (Cl) with depth greater than or equal to l to prevent dimension mismatches: θlg = (1/|Cl|) ∑ θli.
• Qubit-Aware Embedding: Embedding the quantum state (ρi) from a client with fewer qubits into a larger, common Hilbert space using a mapping (Ui) before aggregation: ρ̃i = UiρiU†i.
• Circuit Compression: Using lightweight approximations of complex quantum circuits, such as through gate pruning or variational approximation, to allow low-resource devices to participate in training.
3.3 Hardware-Aware Mitigations
These solutions account for the physical differences in client hardware capabilities.
• Hybrid Quantum–Classical Integration: Allowing low-resource clients to delegate computationally intensive tasks to classical layers while still using quantum layers for feature extraction.
• Personalized Synchronization: Synchronizing only a subset of globally compatible parameters (ωtg) while allowing other parameters (ωti) to be customized locally on each client device, balancing alignment with a regularization factor λ: ωt+1i = ωti − η(gti + λ(ωti −ωtg)).
• Fairness-Aware Weighting: Scaling client contributions based on their effective hardware capacity, such as qubit count (qi) and gate fidelity (ϕi), to prevent high-capacity devices from dominating the global model: wi = (qi·ϕi) / ∑(qj·ϕj).
3.4 Noise-Resilient Strategies
These methods are designed to counteract the destabilizing effects of inconsistent quantum noise.
• Noise-Aware Aggregation: Weighting client updates (θi) based on their inverse noise variance (σ²i), giving more influence to updates from more stable, less noisy devices: θg = (∑ (1/σ²i)θi) / (∑ (1/σ²i)).
• Sporadic Participation: Allowing only clients whose local accuracy (A(t)i) meets a minimum performance threshold (τ) in a given training round to participate in the global aggregation: i ∈ C(t) ⇐⇒ A(t)i ≥ τ.
While these strategies have greatly improved the robustness of general QFL systems, the progression of the field has opened a new frontier focused on more specialized applications, giving rise to the next major challenge: facilitating effective cooperation in multi-agent quantum systems.
4. The Next Frontier: The Challenge of Distributed Cooperation in QMARL
As QFL frameworks matured, a specialized and highly promising area emerged: Quantum Multi-Agent Reinforcement Learning (QMARL). This subfield aims to train multiple intelligent agents to collaborate on complex tasks. With this evolution came the next great challenge on the timeline—moving beyond mitigating passive system differences to actively engineering efficient cooperation.
The core challenge in any distributed multi-agent environment is balancing the need for agent coordination against the communication overhead and computational cost required to share information. To learn a group policy, agents must have some awareness of each other’s states or actions. However, constant classical communication can quickly become a bottleneck, negating the speed advantages of quantum computation.
Prior QMARL frameworks have been limited in their approach to this problem. They have predominantly relied on classical methods for coordination, such as:
• Using classical communication channels to transmit local observations.
• Employing shared replay buffers where agents pool their experiences.
• Relying on centralized global networks that process all agent data.
The key critique of these approaches is that they under-utilize the intrinsic quantum resources available in a QMARL setting. Specifically, they treat the quantum components as mere replacements for classical neural networks but fail to leverage the quantum channel and the phenomenon of entanglement as a direct medium for cooperation. This limitation inspired the development of a novel framework designed to harness these uniquely quantum properties to solve the cooperation problem.
5. A Frontier Solution: Leveraging Quantum Entanglement via the eQMARL Framework
The entangled QMARL (eQMARL) framework was proposed as a novel solution to the cooperation challenge, fundamentally redesigning how agents collaborate. Its unique architecture facilitates coordination directly over a quantum channel by leveraging entanglement, thereby eliminating the need for agents to share their local environmental observations.
The core architectural components of the eQMARL framework are:
1. Entangled Split Critic: The framework deploys a joint value function estimator, known as a quantum critic, that is physically spread across the agents. Each agent hosts a local branch of this critic network in the form of a Variational Quantum Circuit (VQC).
2. Joint Input Entanglement: A trusted central server prepares an entangled input state that couples the agents’ local critic branches. This is achieved using a variation of Bell state entanglement, creating a quantum mechanical link between the agents’ VQCs over a quantum channel.
3. Decentralized Observation Encoding: Each agent independently collects its local observation from the environment. It then encodes this observation into its assigned qubits using its local VQC branch. Crucially, the observation itself is never transmitted.
4. Centralized Joint Measurement: The locally-encoded qubits from all agents are sent back to the central server. The server performs a joint measurement across all qubits simultaneously to estimate a single, joint value for the collective observations of all agents.
The impact of this architecture is transformative. It dramatically reduces classical communication overhead, as only minimal information (rewards and partial gradients) is transmitted classically. It also minimizes the computational burden on the central server and, most importantly, eliminates the need to share local observations, enhancing both privacy and efficiency. This design represents a paradigm shift from using classical communication for coordination to leveraging the physical properties of quantum mechanics itself.
6. Validating the Frontier: Performance and Implications of Entangled Cooperation
To be considered a viable solution, the theoretical advantages of the eQMARL framework required empirical validation against established baselines. Its performance was tested in various multi-agent environments, including CoinGame, CartPole, and MiniGrid, under conditions of both full information (Markov Decision Process, or MDP) and partial information (Partially Observable MDP, or POMDP).
The key experimental findings demonstrate a clear performance advantage for eQMARL when compared to its baselines: a split classical framework (sCTDE) and a fully centralized quantum framework (qfCTDE). The results are summarized below.
These results validate that leveraging entanglement as a medium for cooperation is not only feasible but also highly effective. The eQMARL framework demonstrates that agents can learn a superior cooperative strategy faster and more efficiently, without the privacy and overhead costs associated with classical coordination methods.
7. Conclusion: The Trajectory of Challenges and Future Research Directions
The developmental trajectory of distributed quantum machine learning is a clear and logical progression of problem-solving. The initial privacy and communication overhead of centralized QML led to the creation of the QFL architecture. The practical deployment of QFL then revealed the deep-seated challenge of data and system heterogeneity, prompting the development of a suite of targeted mitigation strategies. Finally, the push toward more advanced applications like multi-agent systems introduced the problem of efficient cooperation, which was addressed by pioneering the use of quantum entanglement in frameworks like eQMARL.
This journey from one challenge to the next highlights the field’s dynamic nature and points toward the next set of hurdles on the horizon. Based on the limitations of current techniques, several open research topics will define the future of distributed quantum learning:
• Scalability and Robustness: There is a pressing need for more adaptable and noise-resilient algorithms that can maintain learning efficiency in large-scale quantum networks with diverse clients, while preserving privacy and communication efficiency.
• Advanced Error Mitigation: Future QFL frameworks must integrate sophisticated quantum error correction with innovative error-aware learning algorithms to address not only hardware-level errors but also the aggregate errors that arise during federated training.
• Impact of Quantum Network Dynamics: Quantum networks are subject to unique dynamics, such as decoherence-induced latency and entanglement generation failures. Investigating how these quantum-specific network properties affect the stability and performance of QFL systems is critical for designing more robust architectures.
Cast of Characters
1. Introduction: The Stage and the Saga
The emerging field of distributed Quantum Machine Learning (QML) is a new frontier, a complex and exciting stage populated by a fascinating cast of concepts, challenges, and technologies. This guide serves as a dramatis personae for this unfolding technological narrative, defining the key players—the heroes, villains, and fundamental forces—that are shaping its plot. We will explore two primary sagas: the quest for robust Quantum Federated Learning (QFL) amidst the imperfections of real-world quantum hardware and data, and the pioneering of cooperative Quantum Multi-Agent Reinforcement Learning (QMARL) by harnessing fundamental quantum phenomena. Understanding these characters is essential for anyone seeking to navigate the future of decentralized, intelligent systems and to appreciate the intricate drama playing out at the intersection of quantum computing and artificial intelligence.
2. The Protagonists: Core Learning Paradigms
At the heart of our story are two protagonist paradigms: Quantum Federated Learning (QFL) and Entangled Quantum Multi-Agent Reinforcement Learning (eQMARL). These frameworks represent ambitious efforts to combine the power of quantum computing with the principles of distributed machine learning, each aiming to solve critical problems of privacy, scale, and cooperation. While they share a common quantum foundation, their missions and methods are distinct, leading them on different but equally compelling journeys.
2.1. Quantum Federated Learning (QFL): The Decentralized Idealist
• Character Role: QFL is a paradigm that synergizes quantum computing with federated learning. Its purpose is to perform machine learning tasks across distributed networks of quantum devices, enabling collaborative model training without centralizing sensitive client data, thereby preserving privacy.
• Modus Operandi: The QFL protocol follows a precise, four-step procedure for each round of collaborative learning:
1. Quantum Encoding: Clients transform their classical local data into quantum states for processing. This is a crucial first step, using methods such as basis, amplitude, phase, or entanglement encoding to represent classical information in the language of qubits.
2. Local Model Training: Each client independently trains a local quantum or hybrid quantum-classical model. These models, often implemented as Variational Quantum Circuits (VQCs) or Quantum Neural Networks (QNNs), learn from the client’s local data.
3. Quantum Model Sharing: Clients share their trained local models with a central server for aggregation. This can be done through two distinct channels. Using classical channels, clients extract and transmit classical parameters (like the rotation angles of quantum gates). Using quantum channels, clients can directly transfer the quantum states of their models via quantum teleportation, preserving quantum correlations like entanglement.
4. Quantum Model Aggregation: The central server integrates the local models into an improved global model. Similar to sharing, this can be a classical parameter aggregation (using algorithms like FedAvg to average gate angles) or a more advanced quantum state aggregation that directly combines the quantum states to maintain coherence.
• Core Motivation: QFL’s primary mission is to leverage the unique benefits of quantum computation—such as faster processing and more effective handling of complex data—to enhance the efficiency and scalability of decentralized learning, all while upholding the core federated promise of data privacy.
2.2. Entangled QMARL (eQMARL): The Cooperative Innovator
• Character Role: eQMARL is a novel distributed actor-critic framework for multi-agent reinforcement learning. It is engineered to foster deep collaboration between learning agents by leveraging a quantum channel as an active coordination medium, not just a data pipe.
• Core Innovation: eQMARL’s defining feature is its use of a quantum entangled split critic. In this unique architecture, the critic network—which evaluates the agents’ actions—is physically spread across the agents. The individual branches of this critic are coupled not by classical messages, but through entangled input qubits prepared by a central server. This allows agents to coordinate implicitly, their learning processes intrinsically linked by a fundamental quantum property.
• Key Advantages: This innovative approach yields several significant benefits:
◦ Eliminates Observation Sharing: Entanglement serves as the coordination medium, allowing agents to cooperate effectively without ever needing to explicitly share their local environmental data with each other or a central server, thus enhancing privacy and efficiency.
◦ Reduces Communication Overhead: By using the quantum channel for coordination, the framework significantly cuts down on the classical communication required by other MARL approaches, which often rely on transmitting intermediate model activations or raw observations.
◦ Minimizes Centralized Burden: Agent policies are tuned via joint quantum measurements performed at the central server. This drastically reduces the server’s computational load, requiring it to learn only a single scaling parameter, a stark contrast to baselines that need large, centralized neural networks.
• Core Motivation: eQMARL’s mission is to exploit quantum phenomena—specifically entanglement and the quantum channel—as untapped resources. It aims to achieve faster, more efficient, and more private cooperation in complex multi-agent systems, demonstrating that quantum properties can be a solution, not just a platform, for advanced AI challenges.
As these protagonists strive to achieve their ideals, they face a formidable and multifaceted adversary that threatens to undermine their very foundations.
3. The Central Conflict: The Challenge of Heterogeneity
The primary antagonist in the saga of distributed quantum systems is Heterogeneity. Unlike in classical systems where this challenge is primarily rooted in data distributions and compute power, quantum heterogeneity is a multi-faceted foe, arising from inconsistencies in both the quantum data being processed and the quantum hardware itself. This variability can destabilize training, slow convergence, and degrade model performance, making it the critical obstacle that our protagonists must overcome to achieve robust, scalable, and practical operation.
3.1. Data Heterogeneity: The Shapeshifter
• Character Profile: Data heterogeneity in QFL manifests as differences in the quantum data representations among clients. Even if they start with identical classical information, variations in encoding or hardware can cause their quantum states to diverge, making it difficult to find a common ground for learning.
• Quantum vs. Classical Conflict: The battle against data heterogeneity in the quantum realm is fundamentally different from its classical counterpart. The unique laws of quantum mechanics introduce new rules of engagement.
• Manifestations: This antagonist appears in several forms:
◦ Heterogeneous Quantum Encoding: This occurs when clients use different methods to encode their data (e.g., amplitude vs. phase encoding) or apply different pre-treatment steps before encoding. The result is a set of inconsistent quantum state representations that are difficult to aggregate into a coherent global model.
◦ Multimodal Data: This challenge arises when different clients contribute varied types of inputs, such as quantum states from a sensor, classical text, and images. Integrating these disparate modalities can skew the global model, biasing it towards clients with richer or higher-quality data.
3.2. System Heterogeneity: The Brute Force
• Character Profile: System heterogeneity represents the brute-force challenges imposed by physical variances in quantum hardware and model architectures across the client network. No two quantum devices are perfectly alike, and these differences directly impact performance.
• Manifestations: This challenge takes shape through several physical limitations:
◦ Heterogeneous PQC Architecture: Due to hardware constraints, clients may use Parameterized Quantum Circuits (PQCs) of varying depths and complexity. This mismatch complicates the process of global model aggregation and raises fairness issues, as clients with more powerful hardware may disproportionately influence the final model.
◦ Varying Number of Qubits: The number of available qubits differs across devices, directly limiting the computational power and data representation capabilities of certain clients. This creates an imbalance in what each client can contribute to the federated task.
◦ Inherent Quantum Noise: Every quantum device has a unique noise profile, leading to inconsistent model updates. This noise comes from three primary sources: Decoherence, the loss of a qubit’s quantum state due to environmental interaction; Gate Noise, errors that occur during quantum operations due to hardware faults; and Measurement Irregularities.
To defeat this powerful antagonist, our protagonists must rely on a set of specialized allies and a well-stocked armory of strategies.
4. The Allies & Armory: Enablers and Solutions
To confront the challenge of heterogeneity and pioneer new forms of cooperation, QML frameworks cannot fight alone. They rely on a specialized set of tools and fundamental quantum properties that act as powerful allies. The core concepts of Quantum Entanglement and the Quantum Channel serve as key enablers, providing capabilities not found in the classical world. Alongside them, a growing arsenal of Mitigation Strategies provides the specific weaponry needed to combat the disruptive effects of heterogeneity in QFL.
4.1. The Mystical Force: Quantum Entanglement
• Definition: Quantum entanglement is a fundamental property of quantum mechanics where the states of two or more qubits become intrinsically linked. This connection persists even when the qubits are physically separated, meaning an action on one instantaneously influences the other.
• Role in eQMARL: In the eQMARL framework, entanglement is the crucial coordination medium. It is used to couple the split critic VQCs across different agents, effectively weaving their individual learning processes together. This allows them to implicitly coordinate their policies and learn cooperative strategies without needing to classically communicate their private observations. To establish this connection, the framework can employ any of the four fundamental two-qubit entanglement schemes known as the Bell states (Φ+, Φ−, Ψ+, and Ψ−). While all are viable, experimental results demonstrate that the Ψ+ state provides a clear advantage in convergence speed and final score, establishing it as the most effective ally for eQMARL’s cooperative mission.
4.2. The Conduit: The Quantum Channel
• Definition: A quantum channel is a communication medium that allows for the direct transfer of quantum states (qubits). Unlike a classical channel that transmits bits (0s and 1s), a quantum channel preserves delicate quantum properties like coherence and entanglement during transmission.
• Role in QFL and eQMARL: This conduit plays a vital role in both protagonist frameworks. In QFL, it enables an advanced form of model sharing where entire quantum models can be transferred via quantum teleportation. In eQMARL, it is the essential medium for the central server to distribute entangled qubits to the agents, establishing the foundational link for the split critic architecture.
4.3. The Toolkit: Mitigation Strategies for QFL
• Overview: To combat the specific data and system-level inconsistencies in QFL, researchers have developed a toolkit of mitigation strategies. These techniques are designed to harmonize clients and stabilize the federated learning process in the face of quantum-specific heterogeneity.
• Strategic Categories: The arsenal is organized into four main categories:
◦ Encoding-Level Mitigations: These strategies address Hilbert space incompatibility by aligning quantum data distributions, using techniques like Encoding-Aware Weighting to prioritize clients with more consistent data representations.
◦ Model-Architecture Strategies: To handle mismatched PQC structures or qubit counts, these approaches use methods such as Layer-Wise PQC Aggregation to ensure only compatible model layers are combined.
◦ Hardware-Aware Mitigations: These strategies account for device-level limitations like qubit counts and gate fidelities, employing techniques like Fairness-Aware Weighting to scale client contributions based on their hardware capacity.
◦ Noise-Resilient Strategies: To counter the effects of decoherence, gate errors, and measurement noise, these approaches use methods such as Noise-Aware Aggregation to weight client updates based on their inverse noise variance, giving more credence to updates from stable devices.
Armed with these allies and tools, our protagonists can be instantiated in the real world as concrete, high-performing frameworks.
5. Featured Players: The Frameworks in Action
The abstract concepts and strategies come to life through specific, “featured” characters—fully realized frameworks that demonstrate how these components are assembled into functional, high-performing systems. SPQFL and the eQMARL architecture serve as two such concrete examples, each showcasing a successful implementation that directly addresses the core challenges of its respective domain.
5.1. SPQFL: The Resilient Hero
• Identity: The Sporadic Personalized Quantum Federated Learning (SPQFL) protocol is a case study in resilience, specifically designed to tackle the twin challenges of quantum noise and non-IID data distributions that plague real-world QFL deployments.
• Key Abilities: SPQFL’s success stems from two primary design choices that allow it to adapt and thrive in heterogeneous environments:
1. Regularization-Based Personalization: This mechanism penalizes overfitting on local client data, which helps to stabilize the training process for clients with diverse data distributions and prevents their local models from diverging too far from the global objective.
2. Sporadic Learning Mechanism: This adaptive filter selectively allows only those clients who meet a minimum validation accuracy threshold to participate in the global aggregation. This prevents noisy or sub-par updates from low-quality devices or difficult data splits from polluting and degrading the shared global model.
• Accomplishments: The combination of these abilities leads to significant performance gains. Compared to a regular QFL baseline, SPQFL demonstrates superior accuracy across multiple benchmark datasets, achieving improvements of 3.03% on MNIST, 2.51% on FashionMNIST, 3.71% on CIFAR-100, and 6.25% on Caltech-101.
5.2. The eQMARL Architecture: The Cooperative Team
• Team Roster: The eQMARL framework operates as a tightly integrated team, with each component playing a specialized role to achieve novel, entanglement-driven cooperation.
◦ The Decentralized Agents: Stationed at the edge, these are the actors of the system. They interact with the environment, execute a local actor policy, and encode their local observations into their respective branch of the quantum critic.
◦ The Split Quantum Critic: This is the innovative heart of the system. It is not a single entity but a distributed network composed of local VQC branches, one on each agent. These branches are physically separate but computationally coupled via entanglement.
◦ The Central Server: In eQMARL, the server’s role is transformed. Instead of performing heavy computations or storing a large centralized model, its primary jobs are to prepare the entangled input states for the agents and to perform joint quantum measurements across all qubits to estimate the joint value function. This minimalist approach drastically reduces its parameter load.
• Rival Comparison: The eQMARL team’s unique strategy delivers a clear performance advantage. In experiments, eQMARL using Ψ+ entanglement converges up to 17.8% faster and achieves a higher overall score compared to both a split classical (sCTDE) rival and a fully centralized quantum (qfCTDE) baseline. Remarkably, it achieves this while requiring 25-times fewer centralized parameters than the sCTDE approach, demonstrating a dramatic increase in efficiency.
These featured players, in turn, are built upon a foundation of fundamental components that make all of quantum machine learning possible.
6. The Supporting Cast: Fundamental Components
The protagonists and their armory of tools are all built upon a foundation of essential quantum concepts. These supporting characters are the fundamental units, operations, and models that form the bedrock of quantum machine learning. Without them, the entire saga could not take place.
• Qubits: The quantum bit, or qubit, is the fundamental unit of quantum computation. Unlike a classical bit, which can only be a 0 or a 1, a qubit can exist in a superposition of both states simultaneously. This property allows quantum computers to process a vast number of possibilities at once.
• Quantum Gates: Quantum gates are the basic operations that manipulate the states of qubits. They are reversible and act on the superposition of states. Common examples include the Pauli-X (a quantum NOT gate), the Hadamard gate (used to create superposition), and the CNOT gate (used to create entanglement between two qubits).
• Variational Quantum Circuits (VQCs): VQCs are the quantum analog of neural network layers and serve as the core learning engine in both QFL and eQMARL models. They are composed of a sequence of quantum gates, some of which are parameterized (like rotation gates) and can be “tuned” during training, and others that are fixed (like entangling gates). By optimizing these parameters, a VQC can learn to solve complex problems.
• Quantum Clients / Decentralized Agents: These are the distributed entities that perform local computation. Though their context differs, their role is fundamentally similar. In QFL, they are known as Quantum Clients, responsible for encoding local data and training local models. In eQMARL, they are Decentralized Agents, tasked with executing policies in an environment and housing the individual VQC branches of the split critic.
7. Conclusion: The Unfolding Saga
The cast of characters presented here—from high-level paradigms like QFL and eQMARL to the central antagonist of Heterogeneity and the fundamental forces of Entanglement and Quantum Channels—are locked in a dynamic interplay that is driving innovation at the quantum frontier. We have seen how protagonists like SPQFL and eQMARL leverage unique quantum properties and clever strategies to overcome significant challenges, pointing toward a future of more powerful, private, and cooperative intelligent systems.
However, the saga is far from over. Significant challenges remain, and the plot continues to thicken. The next chapters in this ongoing story will likely be written by researchers exploring critical open questions, seeking to push the boundaries of what is possible. The key research topics that will shape the future include:
• Scalability and Robustness Enhancements: Developing more adaptable and noise-resilient algorithms that can maintain learning efficiency across large-scale quantum networks with diverse client capabilities.
• Advanced Error Mitigation Techniques: Creating novel error-aware learning algorithms and integrating quantum error correction directly into distributed frameworks to combat both hardware-level noise and the aggregate errors that arise during federated training.
• Impact of Quantum Network Dynamics: Investigating how unique quantum network phenomena—such as decoherence-induced latency and entanglement generation failures—affect the stability and performance of distributed QML systems, leading to more robust, communication-aware protocols.
FAQ
1.0 The Fundamentals of Quantum Federated Learning (QFL)
Quantum Federated Learning (QFL) represents a groundbreaking convergence of quantum computing and distributed machine learning. Its strategic importance lies in its ability to enable privacy-preserving, high-performance model training on sensitive, decentralized data. By leveraging the unique properties of quantum mechanics, QFL aims to solve complex computational problems that are beyond the reach of classical federated systems.
--------------------------------------------------------------------------------
1.1 What is Quantum Federated Learning (QFL)?
Quantum Federated Learning (QFL) combines quantum computing with federated learning (FL) to perform machine learning tasks across distributed networks. Its primary goal is to enable multiple clients to collaboratively train a shared model without centralizing their raw data, thus preserving privacy. QFL leverages fundamental quantum properties like superposition and entanglement to enhance computational efficiency and scalability, making it possible to handle complex, large-scale datasets more effectively than classical methods.
1.2 How is QFL different from traditional Quantum Machine Learning (QML)?
The key difference lies in the data handling and network architecture. Conventional Quantum Machine learning (QML) frameworks typically require data to be collected and processed on a central server. This centralized approach raises significant privacy concerns and creates substantial communication overhead when transferring high-dimensional data. QFL was developed to overcome these limitations. By training models locally on decentralized devices and only sharing model updates, QFL provides inherent data privacy and is better suited for practical scenarios involving continuous streams of sensitive information.
1.3 What are the core components of a quantum computing system used in QFL?
The foundational elements of quantum computation that enable QFL include:
• Quantum bit (qubit): The fundamental unit of quantum information. A qubit can hold the values 0 and 1 simultaneously through superposition and can be linked with other qubits through entanglement, where the state of one qubit is intrinsically connected to the state of another, regardless of physical distance.
• Quantum gates: These are the basic, reversible operations that manipulate the states of qubits. Common examples include the Pauli-X gate (a quantum version of the classical NOT gate), the Hadamard gate (used to create superposition), and the CNOT gate (used to create entanglement).
• Quantum layer: A sequence of quantum operations, typically composed of parameterized and entangling quantum gates, used within variational quantum circuits (VQCs). A quantum layer functions as the quantum equivalent of a neural network layer, allowing models to learn complex data patterns.
• Quantum measurement: The process of extracting a classical result (either 0 or 1) from a qubit. Since a qubit exists in a superposition of states, measurement collapses this superposition into a single, definite value that can be used for classical computations.
1.4 How does a typical QFL system work?
A standard QFL system operates through a four-stage procedure:
1. Quantum Encoding: Classical data from each client is transformed into quantum states that a quantum computer can process. Common methods include basis, amplitude, phase, or entanglement encoding.
2. Local Model Training: Each client uses its local data to train a quantum or hybrid quantum-classical model, often using architectures like Variational Quantum Circuits (VQCs) or Quantum Neural Networks (QNNs).
3. Quantum Model Sharing: The trained local models, or more commonly their parameters, are sent to a central server. This can be done via classical channels, which is practical but loses quantum correlations, or via quantum channels, which preserve quantum coherence but are more resource-intensive.
4. Quantum Model Aggregation: The central server integrates the local models to create an improved global model, using methods like classical parameter averaging (Federated Averaging) or by directly aggregating quantum states.
While this process describes the ideal operation of a QFL system, real-world implementations are complicated by the profound challenge of heterogeneity across quantum clients.
2.0 The Core Challenge: Heterogeneity in QFL
Heterogeneity is the primary obstacle to deploying robust, scalable, and practical Quantum Federated Learning systems. Unlike in classical computing, where heterogeneity typically relates to differences in data distribution and processing power, heterogeneity in QFL is deeply rooted in the fundamental properties of quantum hardware, data representation, and noise. This creates a unique and complex set of challenges that require specialized solutions.
--------------------------------------------------------------------------------
2.1 What does “heterogeneity” mean in the context of QFL?
In QFL, heterogeneity refers to the inherent variability across the distributed quantum clients participating in the learning process. These inconsistencies can disrupt training stability, slow down convergence, and degrade the performance of the final global model. The source material classifies these variances into two main categories: data heterogeneity and system heterogeneity.
2.2 How does QFL heterogeneity differ from heterogeneity in classical Federated Learning?
QFL introduces unique challenges that have no direct equivalent in classical Federated Learning (FL). The fundamental differences stem from the physics of quantum information and hardware.
2.3 What is Data Heterogeneity in QFL?
Data heterogeneity refers to differences in how quantum data is represented and structured among clients, which can occur even when clients start with identical classical data. The two primary causes are:
• Heterogeneous Quantum Encoding: Clients may use different methods (e.g., amplitude vs. phase encoding) or the same method with different pre-processing techniques to convert classical data into quantum states.
• Multimodal Data: Clients may manage varied types of data inputs, such as quantum states from sensors alongside classical data like text or images.
These differences lead to inconsistent feature spaces, where local models extract divergent quantum representations. This causes training instability and can skew the global model toward clients with more dominant data modalities.
2.4 What is System Heterogeneity in QFL?
System heterogeneity arises from variances in the quantum hardware, architecture, and environmental conditions across different clients. The three main causes are:
• Heterogeneous PQC Architecture: Clients may use Parameterized Quantum Circuits (PQCs) with different depths or structural complexity due to hardware limitations or design choices.
• Varying Number of Qubits: Clients often possess different numbers of available qubits, which directly impacts their computational capacity. Because quantum encoding maps classical data into quantum states, clients with fewer qubits cannot adequately represent high-complexity data and are restricted from implementing more expressive quantum circuits, leading to less powerful local models and inconsistent parameter dimensions during aggregation.
• Inherent Quantum Noise: Each quantum device experiences unique noise patterns. This includes discrepancies in decoherence (loss of quantum state), gate noise (imperfections in quantum operations), and measurement irregularities.
The collective impact of these factors includes computational imbalances, inconsistent model updates, and slower convergence of the global model. The profound differences between classical and quantum heterogeneity make it clear that simply adapting existing FL solutions is insufficient. The next section explores a new class of mitigation strategies, specifically engineered to address these unique quantum challenges at their source.
3.0 Strategies for Mitigating Heterogeneity
To bridge the gap between theoretical QFL and practical deployment, researchers have developed a multi-layered defense against heterogeneity. These strategies operate at different levels of the QFL stack—from standardizing quantum data representations to compensating for the physical imperfections of hardware—to create a more resilient and cohesive learning environment. They are broadly categorized as encoding-level, model-architecture, hardware-aware, and noise-resilient solutions.
--------------------------------------------------------------------------------
3.1 What are Encoding-Level and Model-Architecture strategies?
These strategies focus on addressing the data heterogeneity caused by inconsistent quantum data representations and the system heterogeneity arising from mismatched model structures.
• Encoding-Level Mitigations:
◦ Encoding Harmonization: Aims to align quantum data distributions by standardizing classical inputs before they are encoded into quantum states.
◦ Encoding-Aware Weighting: Adjusts the influence of each client’s contribution during aggregation based on the similarity of their quantum state representations to a global reference.
• Model-Architecture Strategies: To address the system heterogeneity caused by clients using PQCs of varying depths or possessing different numbers of qubits (as detailed in Section 2.4), several strategies have been proposed to ensure model compatibility:
◦ Layer-Wise PQC Aggregation: To handle clients with different PQC depths, this method aggregates only the parameters from layers that are shared by all clients, thereby avoiding dimension mismatches.
◦ Qubit-Aware Embedding: For clients with fewer qubits, their quantum states are embedded into a larger, shared Hilbert space, allowing their models to be aggregated with those from more powerful clients.
◦ Circuit Compression: Allows low-resource devices to participate by using lightweight approximations of complex quantum circuits, reducing their computational burden.
3.2 What are Hardware-Aware and Noise-Resilient strategies?
These strategies are designed to manage the physical variances in quantum hardware and the inherent, device-specific noise that affects quantum computations, both key drivers of system heterogeneity.
• Hardware-Aware Mitigations:
◦ Hybrid Quantum–Classical Integration: Allows clients with limited quantum resources to offload complex computations to classical layers, using their quantum hardware only for tasks like feature extraction.
◦ Personalized Synchronization: Instead of enforcing a single global model, clients synchronize only globally compatible parameters while allowing other parts of the model to be customized locally.
◦ Fairness-Aware Weighting: Prevents high-capacity devices from dominating the training process by scaling their contributions based on hardware metrics like qubit count or gate fidelity.
• Noise-Resilient Strategies:
◦ Noise-Aware Aggregation: Weights client updates based on their inverse noise variance, giving more influence to updates from more stable, less noisy devices.
◦ Sporadic Participation: Establishes a performance threshold and allows only clients who meet it to participate in global aggregation, preventing unstable updates from corrupting the global model.
The Sporadic Personalized Quantum Federated Learning (SPQFL) protocol offers a practical case study of how several of these mitigation strategies can be combined to achieve robust performance in a heterogeneous environment.
4.0 Case Study: SPQFL for Noise and Data Heterogeneity
The Sporadic Personalized Quantum Federated Learning (SPQFL) protocol is a concrete application designed to jointly tackle the critical challenges of quantum noise and non-IID data distributions. It demonstrates how tailored mitigation strategies can lead to significant performance improvements in real-world QFL deployments.
--------------------------------------------------------------------------------
4.1 What is Sporadic Personalized QFL (SPQFL)?
SPQFL is a specialized protocol designed to enhance the robustness and accuracy of QFL systems. By directly and simultaneously addressing both system-level heterogeneity (quantum noise) and data-level heterogeneity (non-IID distributions), it delivers consistent accuracy gains and faster convergence compared to other QFL frameworks.
4.2 How does SPQFL work?
SPQFL combines two core mechanisms to achieve its superior performance:
1. Sporadic Learning: This is a selective participation mechanism that acts as a quality filter. Only clients whose local models achieve a validation accuracy above a predefined threshold (τ) are permitted to submit their updates for global model aggregation. This approach effectively prevents noisy or sub-par updates from degrading the shared global model.
2. Personalization: This mechanism uses a regularization-based approach to balance local model customization with alignment to the global model. It helps stabilize training for clients with heterogeneous data by allowing their local models to adapt to their specific data distributions while still contributing effectively to the collective learning process.
4.3 How effective is SPQFL?
Experimental results show that SPQFL consistently outperforms existing approaches, including standard QFL, Personalized QFL (PQFL), and weighted-personalized QFL (wpQFL), in both classification accuracy and convergence speed. For example, compared to the regular QFL baseline, SPQFL achieved significant accuracy improvements across several benchmark datasets:
• 3.03% on MNIST
• 2.51% on FashionMNIST
• 3.71% on CIFAR-100
• 6.25% on Caltech-101
These results confirm its effectiveness as a scalable and noise-resilient protocol. While SPQFL demonstrates progress in mitigating challenges in QFL, the field is also exploring how to actively leverage unique quantum properties in other distributed systems, as exemplified by the eQMARL framework.
5.0 Advanced Application: Entangled Quantum Multi-Agent Reinforcement Learning (eQMARL)
Moving beyond the challenges of federated learning, the field is also exploring how quantum properties can solve fundamental problems in other distributed AI paradigms like multi-agent reinforcement learning. The Entangled Quantum Multi-Agent Reinforcement Learning (eQMARL) framework exemplifies this, leveraging entanglement not to mitigate unwanted heterogeneity, but to actively enable sophisticated, privacy-preserving collaboration between agents.
--------------------------------------------------------------------------------
5.1 What is the novel eQMARL framework?
eQMARL is a distributed actor-critic framework for multi-agent reinforcement learning that facilitates agent cooperation over a quantum channel. Its key innovation is a quantum entangled split critic, which eliminates the need for agents to share their local observations with each other or a central server. This design dramatically reduces classical communication overhead and lessens the computational burden on the central server.
5.2 How does entanglement enable cooperation in eQMARL?
The mechanism relies on a distributed “split critic” architecture where the critic network is spread across the agents. A central server prepares and distributes entangled input qubits to each agent via a quantum channel. This couples their local variational quantum circuits (VQCs), allowing their policies to be tuned collaboratively through joint quantum measurements performed at the central server. This process enables the system to coordinate agent behavior without any agent ever transmitting its local environmental data. Experiments found that the Ψ+ Bell state was the most effective form of entanglement for facilitating this cooperative learning.
5.3 What are the demonstrated benefits of eQMARL?
The eQMARL framework has demonstrated significant advantages over both classical and non-entangled quantum baseline models in cooperative tasks.
• Faster Convergence: Converges to a cooperative strategy up to 17.8% faster than baseline models.
• Higher Performance: Achieves a higher overall score on average in cooperative tasks.
• Reduced Centralization: Requires a constant factor of 25-times fewer centralized parameters compared to the split classical baseline, as only a single measurement parameter is tuned at the server.
• Privacy by Design: Achieves strong performance without any sharing of local environment observations among agents or with the central server.
This application showcases how quantum properties can be harnessed not just for speed, but for fundamentally new and more efficient distributed AI architectures, underscoring the broad future potential of the field.
6.0 The Future of Heterogeneous QFL
While significant progress has been made in identifying the challenges of heterogeneity in QFL and developing initial mitigation strategies, several open research topics remain critical for enabling the practical, large-scale deployment of these systems. Future work must focus on building more scalable, robust, and error-resilient frameworks that can operate effectively in real-world quantum networks.
--------------------------------------------------------------------------------
6.1 What are the key open research areas in heterogeneous QFL?
To advance the field toward real-world application, researchers need to address the following critical areas:
1. Scalability and Robustness: Developing more adaptable and noise-resilient algorithms that can maintain learning efficiency and privacy in large-scale quantum networks composed of diverse clients.
2. Advanced Error Mitigation: Integrating sophisticated quantum error correction with innovative, error-aware learning algorithms to address not only hardware-level errors on individual devices but also the aggregate errors that accumulate during federated training.
3. Impact of Quantum Network Dynamics: Investigating how unique quantum network properties, such as decoherence-induced latency and entanglement generation failures, affect the stability and performance of QFL systems to develop more robust, communication-aware protocols.
Table of Contents with Timestamps
Introduction: The Quantum-AI Convergence | 00:00 Opening frameworks and the mission to explore the marriage of quantum computing and machine learning, introducing the collaborative research team and the dual challenges of infrastructure and coordination.
Quantum Machine Learning Foundations | 02:35 Understanding the fundamental quantum phenomena—superposition, entanglement, and quantum interference—that enable QML’s computational advantages over classical approaches.
The Centralized Dead End | 04:52 Why conventional centralized quantum machine learning fails due to privacy vulnerabilities, communication bottlenecks, and scalability limitations in distributed environments.
Enter Quantum Federated Learning | 06:34 Introduction to QFL as the solution: keeping data local while sharing only model parameters, combining federated learning principles with quantum computational power.
The Quantum Toolkit: Gates, Circuits, and Encoding | 09:02 Deep dive into the practical mechanisms—quantum gates, variational quantum circuits (VQCs), and encoding strategies—that transform classical data into quantum states.
The Heterogeneity Crisis | 12:38 Confronting the fatal flaw in early QFL: the assumption of homogeneity and how real-world variability in data, hardware, and noise creates catastrophic training instability.
Physics, Not Statistics: The Hilbert Space Problem | 14:01 Understanding why QFL heterogeneity is fundamentally a physics problem, where incompatible quantum states cannot be simply averaged like classical parameters.
Sources of Heterogeneity: Data and Hardware | 14:28 Examining data encoding differences, multimodal challenges, PQC structural variations, and the existential threat of device-specific quantum noise and decoherence.
Engineering Resilience: The Mitigation Framework | 19:14 Layer-by-layer defense strategies including encoding harmonization, architecture-aware aggregation, and noise-resilient weighting mechanisms.
SPQFL: The Breakthrough Protocol | 22:26 Sporadic Personalized Quantum Federated Learning—the innovation that tackles noise and non-IID data through personalization regularization and conditional quality gates.
From Training to Action: Multi-Agent Reinforcement Learning | 25:08 Shifting focus from distributed training infrastructure to applying quantum models for collective decision-making in dynamic, cooperative environments.
The Classical Communication Bottleneck | 26:01 Why classical multi-agent RL suffers from massive communication overhead, privacy breaches, and computational complexity in centralized coordination.
EQMRL: Entanglement as Coordination | 26:42 The revolutionary framework that uses quantum entanglement itself as the coordination mechanism, eliminating the need for classical information sharing.
The Architecture of Implicit Coordination | 27:38 Three-stage process: joint input entanglement, decentralized encoding, and joint measurement that couples agents at the quantum level.
Empirical Validation: Speed, Stability, and Scalability | 30:39 Benchmark results showing 17.8% faster convergence, superior stability, and a staggering 25x reduction in centralized parameters compared to classical baselines.
Mini-Grid Navigation: Coordination in Action | 33:10 Real-world test demonstrating 4.5x higher rewards and 50% faster goal achievement through entanglement-enabled implicit coordination.
The Quantum Future and Open Challenges | 34:48 Synthesizing the journey from theory to implementation and identifying the next generation of research questions in scalability, error mitigation, and network reliability.
Closing Reflections: Frameworks for Understanding | 37:27 Recurring themes of boundary dissolution, adaptive complexity, embodied knowledge, and quantum-like uncertainty as lenses for our modern world.
Index with Timestamps
actor-critic framework, 27:53
aggregation, 08:10, 12:46, 20:44, 22:19
amplitude encoding, 07:26, 10:50, 14:48
Anthropic, 01:03
architecture, 20:30, 20:36
artificial intelligence, 00:55, 35:42, 36:10
Bell state, 28:32
bottleneck, 06:09, 11:15, 26:04, 30:25
centralized training, 05:01, 26:01, 26:57
classical communication, 12:00, 26:08, 27:14, 30:16, 35:51
classical federated learning, 13:31, 19:04, 24:28
client devices, 06:58, 07:08, 08:07
CNOT gate, 09:27, 10:18
coherence, 12:13, 16:51, 37:17
communication overhead, 06:07, 16:31, 17:46, 26:16, 30:16
convergence, 13:26, 30:51, 31:00
coordination, 02:09, 26:01, 26:42, 26:46, 27:01, 27:38, 32:07, 33:26, 34:07, 34:43, 35:18
copyright, 01:03
CPU, 07:08
critic, 28:02, 28:15, 28:20, 35:18
Daru Alexander, 01:13, 26:42, 27:30, 35:12
data distribution, 15:12, 22:42
data encoding, 07:17, 14:34
data privacy, 05:22, 08:29, 08:40
decoherence, 16:32, 18:02, 18:27, 22:32, 24:02, 37:07, 37:17
decentralized execution, 26:57
decentralized networks, 01:22
deep learning, 09:34
defense networks, 08:56
deployment, 00:55, 31:45
edge devices, 07:16, 17:10
Einstein, 04:05
encoding, 07:18, 10:34, 10:42, 11:11, 14:38, 15:00, 19:39, 27:38, 29:06, 29:23, 30:10
entanglement, 02:09, 03:46, 04:13, 04:46, 07:51, 09:30, 10:18, 11:53, 12:23, 18:09, 26:49, 27:30, 28:18, 31:00, 31:29, 34:43, 35:13, 35:18, 35:57, 37:17
entangling gate, 10:18
EQMRL, 02:15, 27:30, 29:02, 30:51, 31:11, 31:28, 32:00, 32:11, 34:04, 34:12, 35:18
error mitigation, 36:43, 36:50
fairness-aware weighting, 21:46
federated learning, 01:44, 06:34, 06:40, 13:31
FedAv, 11:38, 13:55, 14:46
fidelity, 12:20, 18:45, 18:53, 21:53, 21:58
gate fidelity, 16:52, 18:45, 21:54
gate noise, 18:45
gates, 09:11, 09:20, 09:27, 10:18, 10:28
global aggregation, 08:12, 24:13
global model, 08:20, 12:15, 13:21, 16:18, 20:10, 23:10, 23:19, 24:05, 24:12
gradient descent, 10:28
Grian Dinsin, 01:13, 13:02
H-gate, 09:26
hardware, 16:39, 16:46, 17:02, 18:27, 19:30, 21:24, 21:30, 36:02, 36:50
heterogeneity, 01:51, 12:46, 13:11, 13:15, 14:01, 14:22, 16:01, 16:39, 19:20, 35:07
Hilbert space, 14:06, 14:14, 14:36, 15:35, 19:39, 21:09
homogeneity, 12:30, 12:56, 25:03, 35:47
hybrid quantum-classical, 21:30
implicit coordination, 02:09, 27:01, 29:40, 31:10, 33:26, 34:07, 34:26, 34:43, 35:18
inference, 04:13, 04:19
joint measurement, 29:49, 30:31, 32:15
knowledge cutoff, 03:02
lambda, 23:00, 23:06, 23:19, 23:27
latency, 06:15, 37:07
layer-wise aggregation, 20:43
learning, 01:44, 06:34, 08:00, 10:29, 13:31, 21:57, 22:50, 27:30, 27:49
local data, 06:54, 06:58, 23:05, 23:19
local training, 22:52, 23:41
measurement, 04:03, 29:49, 30:31, 32:15, 32:47
Mini-Grid, 33:10, 33:18
MRL, 25:37, 25:42
neural network, 09:36, 09:46, 27:09, 32:01
NISQ devices, 04:43, 07:10, 16:58, 18:02, 31:40
noise, 01:43, 13:09, 13:15, 15:16, 16:18, 16:47, 18:02, 18:45, 19:05, 19:30, 19:38, 22:04, 22:19, 22:28, 22:32, 23:33, 24:15, 25:03, 31:40, 35:07, 36:42, 36:50
noise-aware aggregation, 22:19
non-IID data, 13:40, 22:42, 25:01
observable, 32:47
optimization, 04:26, 08:03
parallelism, 03:37
parameterized gates, 09:57, 10:02, 16:46
parameters, 07:02, 08:09, 10:03, 10:10, 11:34, 12:54, 14:46, 17:15, 18:37, 20:48, 32:29, 35:33
partial observability, 33:27
personalization, 22:55, 23:00, 25:01
phase encoding, 07:26, 11:01, 14:48
policy network, 27:58
POMDP, 30:50
PQC, 16:46, 17:01, 20:36, 20:43
privacy, 02:30, 05:22, 08:29, 08:40, 26:29, 30:04, 30:25, 35:33, 35:43
privacy-preserving, 06:48, 35:42
QFL, 01:51, 06:43, 07:06, 08:29, 08:33, 12:38, 12:46, 13:04, 13:15, 14:01, 14:22, 19:34, 20:54, 24:51, 25:15, 35:07
QML, 02:38, 02:49, 05:01, 05:05
quantum algorithms, 01:20, 08:21
quantum bit, 03:06
quantum channel, 12:00, 12:18, 27:20, 29:02, 29:52
quantum circuits, 09:20, 09:45, 10:11, 16:46, 21:40
quantum communication, 12:11, 26:08
quantum computing, 00:42, 06:50
quantum correlations, 11:53, 29:46
quantum encoding, 10:34, 14:38
quantum federated learning, 01:44, 06:43
quantum gates, 09:11, 18:48
quantum information, 06:03, 10:19, 18:20
quantum interference, 04:13
quantum machine learning, 02:38, 34:54
quantum mechanics, 00:50, 02:09, 27:02
quantum multi-agent reinforcement learning, 02:15
quantum noise, 16:47, 18:02, 22:28, 22:42
quantum parallelism, 03:40
quantum physics, 02:48, 35:56
quantum state, 03:54, 04:03, 10:35, 10:46, 12:06, 12:13, 14:14, 14:29, 14:32, 15:21, 18:08, 20:07, 29:33
quantum teleportation, 12:11
qubit, 03:06, 03:10, 03:22, 04:03, 09:02, 09:58, 16:51, 17:23, 21:08, 21:54, 29:27
Rahman Ratun, 01:13, 06:33, 13:02, 19:10, 22:41, 35:06
rate of change, 16:32, 18:27
reinforcement learning, 02:15, 25:31, 25:37, 27:30
rotational angles, 10:03, 10:10, 11:35
RX gate, 09:58
RY gate, 09:58
RZ gate, 09:58
Saad Waleed, 01:13, 13:03, 26:42, 27:30, 30:38, 35:12
scalability, 05:16, 06:26, 31:45, 32:00, 36:22, 36:40
server, 05:05, 05:39, 07:02, 08:12, 11:35, 11:38, 12:26, 17:46, 20:48, 23:50, 26:01, 28:11, 28:27, 29:02, 29:52, 32:00, 32:03, 32:19, 32:47
SPQFL, 22:32, 24:38, 24:43, 24:51, 35:07
stability, 13:15, 31:11, 31:16, 31:28, 37:24
superposition, 03:02, 03:05, 03:15, 04:13, 07:51, 09:26, 11:54, 18:09, 35:56
system heterogeneity, 16:39
tau, 23:51
Thomas Christo Karisimutal, 01:13, 13:03
threshold, 23:51, 23:54
training, 01:42, 10:28, 13:15, 19:39, 22:52, 23:41, 25:15, 26:01, 26:57, 31:28, 36:55
validation accuracy, 23:51
value function, 28:02, 29:56, 30:00
variational quantum circuit, 09:45, 10:11
VQC, 07:43, 09:45, 11:11, 11:14, 27:09, 28:20, 29:23, 30:09
Poll
Quantum AI & The Future of Technology
Post-Episode Fact Check
VERIFIED CLAIMS:
✓ Quantum Superposition & Entanglement Basics
The podcast’s explanations of quantum superposition (qubits existing in multiple states simultaneously) and entanglement (instantaneous correlation between particles) are accurate and align with established quantum mechanics principles. Einstein did refer to entanglement as “spooky action at a distance” in his criticism of quantum theory.
✓ NISQ Devices
Noisy Intermediate-Scale Quantum (NISQ) devices are indeed the current state of quantum computing technology. These devices are characterized by limited qubit counts (typically 50-1000 qubits), high error rates, and susceptibility to decoherence, as described in the podcast.
✓ Federated Learning Principles
The description of federated learning (FL) keeping raw data local while sharing only model parameters is accurate. Google does use federated learning for features like predictive text, as mentioned in the accompanying essay.
✓ Privacy Vulnerabilities in Centralized Systems
The podcast’s concerns about centralized data collection creating “single points of failure” are well-documented in cybersecurity literature. Major data breaches have validated these concerns repeatedly.
CLAIMS REQUIRING CONTEXT:
⚠ Researcher Names & Collaboration
The podcast mentions researchers: Ratun Rahman, Dinsin Grian, Christo Karisimutal Thomas, Alexander Daru, and Waleed Saad. While these names appear in the source transcript, listeners should note that quantum federated learning and quantum multi-agent reinforcement learning are active research areas with contributions from multiple research groups globally. This episode focuses on specific research threads but represents a broader field of inquiry.
⚠ 17.8% Faster Convergence & 25x Parameter Reduction
These specific performance metrics for EQMRL are presented as research findings. As with all early-stage research, these results are benchmark-specific and may vary significantly depending on the experimental setup, problem domain, and comparison baselines used. These should be understood as promising research results rather than guaranteed performance in production systems.
⚠ Timeline for Practical Deployment
The essay correctly notes “we’re not getting quantum-powered AI assistants next year” and emphasizes the technology is “still in the research phase.” This is accurate. Most experts estimate that practical, scalable quantum AI systems are likely 10-20+ years away, though the exact timeline is subject to significant uncertainty and debate.
TECHNICAL ACCURACY NOTES:
✓ Quantum Gates (Pauli-X, Hadamard, CNOT)
The descriptions of quantum gates are technically accurate. The Pauli-X gate does function as a quantum NOT gate, the Hadamard gate creates superposition, and the CNOT gate creates entanglement between qubits.
✓ Variational Quantum Circuits (VQCs)
The explanation of VQCs as the quantum analog of neural network layers, using parameterized rotation gates (RX, RY, RZ) and entangling gates, correctly represents current quantum machine learning architectures.
✓ Encoding Methods
Amplitude encoding and phase encoding are real quantum data encoding strategies, each with the trade-offs described (compactness vs. processing efficiency).
⚠ Hilbert Space Incompatibility
The podcast’s explanation that heterogeneous quantum states create “Hilbert space mismatch” is conceptually accurate but simplified. In practice, quantum states from different devices exist in the same mathematical Hilbert space, but may have different bases, probability distributions, and quantum properties that make direct aggregation problematic. The analogy of “averaging apples and the color red” effectively communicates the challenge for general audiences.
CONTEXTUAL CONSIDERATIONS:
Hardware Requirements Not Fully Discussed:
The podcast mentions quantum systems need “extreme cooling and isolation” but doesn’t detail that most quantum computers require dilution refrigerators operating at temperatures near absolute zero (15 millikelvin or colder), representing significant infrastructure challenges.
Error Rates:
While decoherence and gate noise are discussed, specific error rates aren’t mentioned. Current NISQ devices typically have gate error rates of 0.1-1%, with coherence times measured in microseconds to milliseconds—constraints that significantly limit practical applications.
Quantum Communication Infrastructure:
The podcast discusses “quantum channels” for transmitting quantum states but doesn’t fully address that quantum communication networks (quantum internet) are themselves in early experimental stages, with only a few operational test networks globally.
Classical Components:
While the hybrid quantum-classical nature is mentioned, the podcast could emphasize more strongly that all current and near-term quantum systems require extensive classical computing infrastructure for control, error correction, and optimization.
CLAIMS ABOUT IMPLICATIONS:
⚠ Privacy Guarantees
The essay states quantum federated learning could provide “privacy-preserving by design” systems. While QFL does improve privacy compared to centralized approaches, it’s important to note that no system provides absolute privacy guarantees. Quantum systems can still be vulnerable to side-channel attacks, implementation flaws, and other security issues.
✓ Surveillance Economy Critique
The essay’s characterization of modern AI as “built on a foundation of centralization and surveillance” is supported by extensive documentation of data collection practices by major technology companies.
⚠ “Physics Makes Better Design Decisions Than Venture Capitalists”
This is editorial commentary rather than a factual claim, though it reflects legitimate concerns about the commercialization pressures affecting technology development priorities.
VERIFICATION SUMMARY:
Overall Accuracy Rating: HIGH
The podcast demonstrates strong technical accuracy in explaining quantum computing principles, federated learning concepts, and the challenges of distributed quantum systems. The researchers’ work is presented in appropriate context as promising early-stage research rather than mature technology.
The accompanying essay appropriately balances optimism about the technology’s potential with realistic acknowledgment of current limitations and timeline uncertainties.
Recommended Listener Takeaways:
The science is real and accurately presented
The technology is genuinely promising but early-stage
Practical applications are years to decades away
The privacy and coordination advantages described are theoretical benefits that would need to be validated at scale
This represents one approach among many being explored in quantum AI
Sources for Further Reading:
Nielsen & Chuang, “Quantum Computation and Quantum Information” (2010)
Preskill, “Quantum Computing in the NISQ era and beyond” (2018)
McMahan et al., “Communication-Efficient Learning of Deep Networks from Decentralized Data” (2017) - Foundational federated learning paper
Recent papers on quantum machine learning in journals like Nature, Science, and PRX Quantum
Fact Check Conducted By: Independent Science Verification
Methodology: Cross-reference with peer-reviewed literature, expert consensus, and current state of quantum computing technology
Last Updated: January 2026